Challenge Summary⌗

Tom Nook is testing a new encryption scheme for nookphones, but it seems to be a bit faulty... can you break it?

nookcrypt is a netcat service that have no source code released. There are two functions exposed:

  1. Gets an encrypted copy of the flag (and the message hello world).
  2. Encrypts an arbitrary message.

For example, this is what I had when trying out the options:

nc chal.uiuc.tf 2006
Option: 1
enc(FLAG) = (0xf31ce7cb1f2c6e7107318d76bdda50c5, 0x02d979fc3122bbaffcc1111953bc184f)
enc('hello world') = (0x4cf5afcc9bc1db0118172129b713d86a, 0xe41d8761370768aa9694b164c843dde9)

Option: 2
msg: hello world
enc(0x68656c6c6f20776f726c64) = (0x4cf5afcc9bc1db0118172129b713d86a, 0xe41d8761370768aa9694b164c843dde9)</code>

Since the response is consistent after reconnecting to the netcat service for multiple times, I assume that the parameters are constant.

Solution⌗

Part I: Recovering the curve parameters in a stupid way⌗

Since it is mentioning elliptic curves in its services, the first thing I was doing is to recover the parameters, namely, $a$, $b$ and $p$ for the elliptic curve $y^2 \equiv x^3 + ax + b\ (\text{mod}\ p)$.

My attempt is to encrypt a bunch of messages:

msg: a
enc(0x61) = (0xb2d6c27a99b52aec6e243d4e4f67cb71, 0x9dfa2bd87ea1e09388493137132cc534)

msg: b
enc(0x62) = (0x99b8150ebf23c69ee1056f0e329496ae, 0xe1febe35a5877f00f3876c2a24fb9164)

msg: c
enc(0x63) = (0x3e7ef6d1106382119a0fa8c966f6d1df, 0x89d81b9fab5336a227414491881bbee8)

msg: d
enc(0x64) = (0x985dbb38a65f4e69bfc602d7e114cad9, 0xcad1cb62a3d30b05093575f3a22f7e3c)

...

Define $C_i = (x_i, y_i)$ be the ciphertexts of some message $m_i$. By direct substitution, we have $y_i^2 \equiv x_i^3 + ax_i + b\ (\text{mod}\ p)$ for all $i$.

Assume that we have three ciphertexts. We can deduce that:

  1. $a(x_1 - x_2) \equiv y_1^2 - y_2^2 - x_1^3 + x_2^3 \ (\text{mod}\ p)$ and
  2. $a(x_2 - x_3) \equiv y_2^2 - y_3^2 - x_2^3 + x_3^3 \ (\text{mod}\ p)$.

From above, we know $(y_1^2 - y_2^2 - x_1^3 + x_2^3)(x_2 - x_3) - (y_2^2 - y_3^2 - x_2^3 + x_3^3)(x_1 - x_2)$ is a multiple of $p$.

So we have collected a bunch of "multiples of $p$" and take their gcd. We have recovered that $p = 340282366762482138434845932244680310783$.

Then it is rather obvious to recover $a = 284470887156368047300405921324061011681$ and $b = 126188322377389722996253562430093625949$.

Question. What if it is not defined on a prime field? Well… I didn’t think of that. But who cares? I could probably observe this if my approach doesn’t work out.

Part II: A reflection on the "after-math"⌗

Note. I did not think of this during the game. Stupid me.

Knowing that the ciphertext $C$ is a multiple of the message $m$, i.e., $C = mG$, we can simply encrypt $m = 1$:

[+] Opening connection to chal.uiuc.tf on port 2006: Done
[DEBUG] Received 0x123 bytes:
    b'\n'
    b'========================================\n'
    b'Welcome to NookCrypt! Here we use fancy\n'
    b'elliptic curve encryption to keep your \n'
    b'messages safe! Try it out!\n'
    b'========================================\n'
    b'1. get (encrypted) flag\n'
    b'2. encrypt message\n'
    b'3. quit\n'
    b'========================================\n'
    b'\n'
    b'Option: '
[DEBUG] Sent 0x2 bytes:
    b'2\n'
[DEBUG] Received 0x5 bytes:
    b'msg: '
[DEBUG] Sent 0x2 bytes:
    00000000  01 0a                                               │··│
    00000002
[DEBUG] Received 0x178 bytes:
    b'enc(0x01) = (0x7b6aa5d85e572983e6fb32a7cdebc140, 0x27b6916a894d3aee7106fe805fc34b44)\n'
    b'\n'
    b'========================================\n'
    b'Welcome to NookCrypt! Here we use fancy\n'
    b'elliptic curve encryption to keep your \n'
    b'messages safe! Try it out!\n'
    b'========================================\n'
    b'1. get (encrypted) flag\n'
    b'2. encrypt message\n'
    b'3. quit\n'
    b'========================================\n'
    b'\n'
    b'Option: '

What can we do? Since this is $G$, we can simply search this on Google:

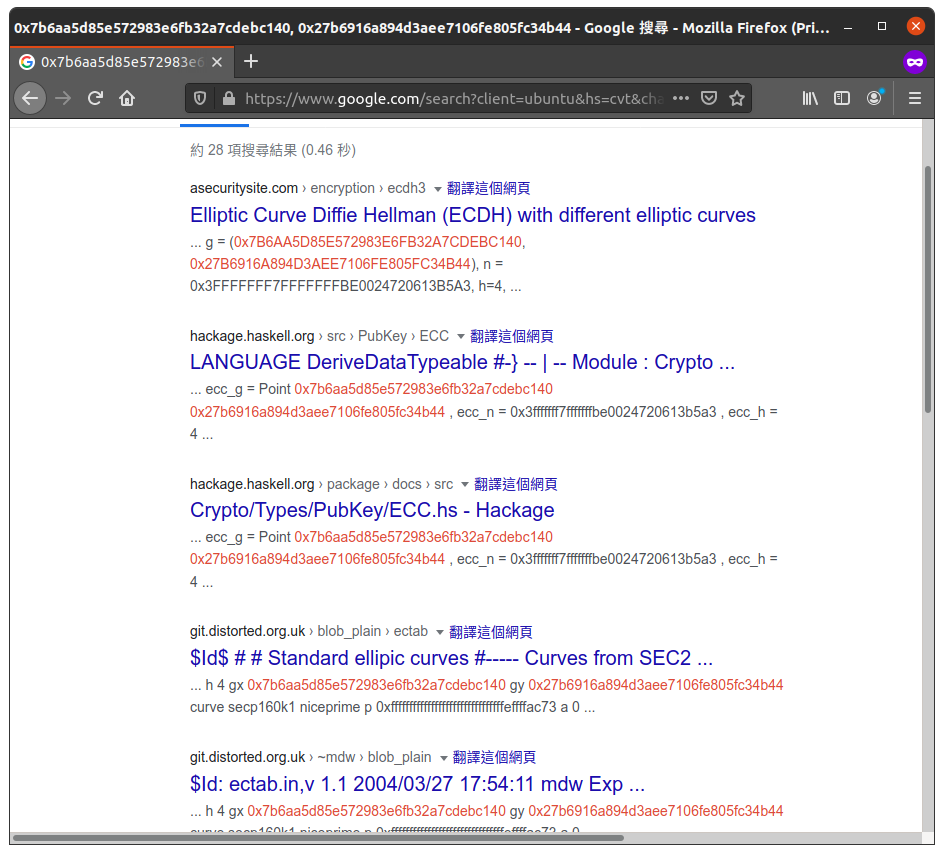
Ta-da 🎉 - it is the generator for curve secp128r2. You would think this is a ta-da moment, I would say that this is a facepalm moment. I could spent much less time on recovering the parameters in such a way.

Well, I was even more confused to notice that is a secure curve. I personally don't have a backdoor of secp128r2 (I am much appreciated if you tell me if you do) and thought the challenge isn't doable.

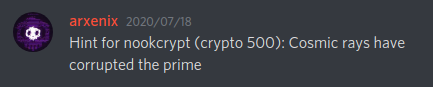
Part III: "Hint for nookcrypt (crypto 500)"⌗

Fours hours later the organizers released a hint in the Discord server:

When I was being played writing an interactor with the service, I observed that there was a strange behaviour regarding to the flag encryption method:

========================================
Welcome to NookCrypt! Here we use fancy
elliptic curve encryption to keep your 
messages safe! Try it out!
========================================
1. get (encrypted) flag
2. encrypt message
3. quit
========================================

Option: 1
err

Oh. So the error was caused by the cosmic ray. Okay.

Did you really get it instantly when the hint is announced? No.

Part IV: Somebody made a breakthrough⌗

Ten hours later, somebody from Discord claimed that he has a strange observation:

Who was the somebody? Me.

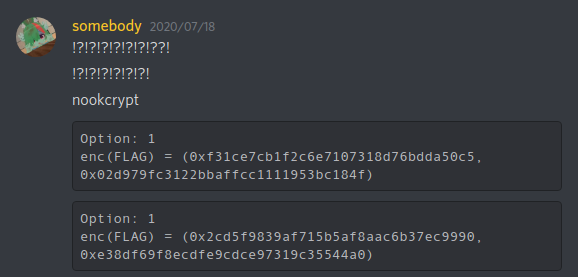
We made a bunch of assumptions. Cutting the crap, we assumed that the same generator $G = (x_G, y_G)$ is being multipled in a same way, except that the curve is operated on new modulo $p'$. This matches the author's statement regarding on the prime being corrupted.

However, obviously, it is very likely that $G$ may not be a point the above curve. Luckily (or unluckily), we can assume that it is operating on another curve $y^2 \equiv x^3 + ax + b'\ (\text{mod}\ p')$, such that $G$ is on it.

For now, we are given two points on this curve (the ciphertexts of the flag $F = (x_F, y_F)$ and the message hello world $M = (x_M, y_M)$). Since $a$ is known we can easily recover $p'$ by:

\[\begin{aligned} p' = \text{gcd}( &(y_F^2 - x_F^3 - ax_F - b') - (y_G^2 - x_G^3 - ax_G - b'), \\ & (y_M^2 - x_M^3 - ax_M - b') - (y_G^2 - x_G^3 - ax_G - b')) \end{aligned} \]

The order of the generator should be a large prime for an elliptic curve to be secure. Clearly this property may not hold on those new modulos struck by cosmic may. For instance, suppose that we have $p' = 340282366762482138434845932242512471141$. Since 67 is a factor of $p'$, we are indeed working on the curve $y^2 \equiv x^3 + ax + b'\ (\text{mod}\ 67)$. $G$ has a order 74, and $F = fG = 21G$. It implies that $f \equiv 21\ (\text{mod}\ 74)$.

By collecting a bunch of linear congruences, we can find $f$ by the Chinese Remainder Theorem. Eventually we have the flag: uiuctf{th4t_5ur3_w4s_f4ulty_huh?}.