Firebird Internal CTF 2021 Writeup

I have written four question for Firebird Internal CTF - Oofbleck (Crypto), Obvious Transfer (Crypto), RC4 (Misc) and Prooof-ooof-Wooork (Reverse, Misc). I will be including all of them in this blog post.

Oofbleck (Crypto)⌗

One (out of six) team have solved this during the CTF period.

Challenge Summary⌗

Some of the block cipher modes of operation are pretty vulnerable, which includes but not limited to padding oracle in CBC, key-recovery attacks with repeated nonces in GCM and Zerologon in CFB8... What about OFB?

Attachments: chall.py, output.txt, secret.py

In this challenge, we are given a ciphertext encrypted with OFB, and the respective encryption script. The following is the core part of the program.

def encrypt(message, key):
    iv = os.urandom(16)
    cipher = AES.new(iv, AES.MODE_OFB, key)
    message = pad(message, 16)
    ciphertext = iv + cipher.encrypt(message)
    return ciphertext

if __name__ == '__main__':
    key = os.urandom(16)
    assert re.match(r'^firebird\{\w{58}\}$', flag)

    ciphertext = encrypt(flag.encode(), key)
    print(base64.b64encode(ciphertext).decode())

Solution⌗

The output feedback mode of operation⌗

Since this is a challenge regarding to the output feedback (OFB) mode, let's see how is it done.

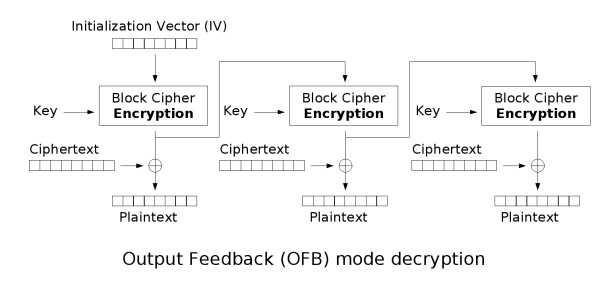
Furthermore, the message is 68 bytes long (firebird{[...58 characters...]}). Since the block size of AES is 16 bytes, it is composed of 5 blocks after padding. Define $(m_1, m_2, m_3, m_4, m_5)$ and $(x_0, c_1, c_2, c_3, c_4, c_5)$ as the padded plaintext and its ciphertext (where $x_0$ is the IV). Then for $i \in {1, 2, 3, 4, 5}$, we have

\[ \begin{cases}\begin{aligned} x_i &= \text{Enc}_k(x_{i-1})\\ c_i &= m_i \oplus x_i \end{aligned}\end{cases} \]

It seems that we have $(x_0, c_1, c_2, c_3, c_4, c_5)$, which does not allow us to recover any of the $m_i$'s... or is it?

Misusing the package methods⌗

Anyone who is familiar with pycrypto (or pycryptodome) may immediately spot the problem - the order of the parameters are messed up. From the documentation¹, the first and the third arguments should be respectively the key and the IV. Unfortunately, they are swapped in this challenge.

Hence, we are actually given $(k, c_1, c_2, c_3, c_4, c_5)$ instead of $(x_0, c_1, c_2, c_3, c_4, c_5)$. Knowing the key, we can recover all of the $x_i$'s given any of them (by either encrypting or decrypting). To retrieve one of the $x_i$'s, let's first look at how the padded plaintext is structured. A 68-byte plaintext will be padded with 12 copies of \x0c under PKCS7 padding. If we let X to be \x0c, the padded message would be:

m1______________ m2______________ m3______________ m4______________ m5______________
firebird{??????? ???????????????? ???????????????? ???????????????? ???}XXXXXXXXXXXX

Since there are only three unknown characters in $m_5$, we can exhaust them to recover $x_5$. Then we can decrypt for $x_4, ..., x_1$ and hence recover $m_4, ..., m_1$. If $m_1$ starts with firebird{, then the flag can be obtained via concatenating the message blocks.

Obvious Transfer (Crypto)⌗

Zero (out of six) teams have solved this during the CTF period.

Challenge Summary⌗

Can you distinguish ciphertext from RSA with random?

nc HOST PORT

Attachments: chall.py, secret.py

We will be given 100 challenges and will win the flag if all of they are all passed. This is how a challenge performed:

c0 = random.getrandbits(1)

print(f'🤯 {i}')

while True:
    params = input('🤖 ').split(' ')
    action = params.pop(0)

    if action == '📦':
        if c0 == 0:
            ciphertext = random.randint(0, k.n-1)
        else:
            ciphertext = int.from_bytes(oaep_k.encrypt(flag), 'big')
        print('🤫', long_to_b64(ciphertext))
    elif action == '🔓':
        c1 = int(params[0])
        if c0 != c1:
            failed = True
        else:
            print('👌')
        break
    elif action == '🏃':
        exited = True
        break
if failed or exited: break

In short, at the beginning of the round, a number $c_0$ is selected. We can request output via 📦 - which outputs a random number if $c_0 = 0$ and a ciphertext from RSA if $c_0 = 1$. Finally we can send our guess $c_1$ via 🔓 - the program terminates if $c_0 \neq c_1$.

Solution⌗

Some trivial variants⌗

There are two variants that make the challenge trivial.

# Variant 1
if c0 == 0:
    ciphertext = random.randint(0, k.n-1)
else:
    # use textbook RSA instead
    ciphertext = pow(int.from_bytes(flag, 'big'), k.e, k.n)

# Variant 2
if c0 == 0:
    ciphertext = random.getrandbits(2048)
else:
    ciphertext = int.from_bytes(oaep_k.encrypt(flag), 'big')

In the first variant, we can use 📦 twice to obtain two ciphertexts, namely $x_1$ and $x_2$. Since there is no randomness involved in encrypting with textbook RSA, $x_1 = x_2$. Of course, it is also possible that $x_1 = x_2$ when $c_0 = 0$. But it is very unlikely and it is neglected.

In the second variant, if $c_0 = 1$, it is always true that $x < n$. On the other hand, if $c_0 = 0$, it is possible that the output to be greater (or equal to) $n$. Thus the probability for $x \geq n$ is

\[p_1 := 1 - \frac{n}{2^{2048}}.\]

Hence, if we call 📦 $k$ times, then the probability for $\text{max}(x_1, x_2, ..., x_k) \geq n$ is

\[p_k := 1 - \left(1 - \frac{n}{2^{2048}}\right)^k.\]

With the results from the experiment, $p_{100} \approx 1.000000$. That said, it is almost certain that there is an $x_i \geq n$ in 100 trials if $c_0 = 0$.

Distinguishing something from random⌗

...of course not! If we cannot distinguish it from random, how about distinguishing random from random? Note that if $c_0 = 0$, the random generated is not cryptographyic secure. They are generated with MT19937 and we can recover its internal state² if we have $624 \times 32$ bits extracted. With that, we can further predict the $c_0$s in the subsequent challenges.

Well... You can take a look at it. I am happy if someone solves the challenge with such an approach, but this is not the intended attack though.

The intended solution⌗

Now suppose that I knew nothing about MT19937 and assumed that the random comes from a CSPRNG. Then the ciphertext for both $c_0 = 0$ and $c_0 = 1$ do not reveal anything useful. Luckily, there is a critical factor - time. It is significantly slower to compute ciphertext when $c_0 = 1$ compared to the case when $c_0 = 0$.

In average, it takes 660µs and 50µs when $c_0 = 0$ and $c_0 = 1$, respectively. We can call 📦 1000 times to overcome network latency and it will be significantly slower if $c_0 = 0$. This way we do not need to crack and recover the states from MT19937.

Prooof-ooof-Wooork (Reverse, Misc)⌗

Four (out of six) teams have solved this during the CTF period.

Challenge Summary⌗

Download the binary, nc HOST PORT, execute the binary, win the flag. That is it. Easy? Easy!

Attachments: gen

When connected to the service, we are given 100 commands to be executed. If we can reply all of the output for the commands in 180 seconds, then the service will grant us the flag. If it is more well-planned, I can simply bribe someone with flags to mine bitcoins.

nc HOST PORT
# This challenge is easy. Just execute the binary to complete the proof-of-work!
# Of course, it will be getting harder and harder...
# ./gen LGb6W/RZCz9KKw== 2223635746 1
# > DfwI12HrGw
# ./gen BlviwtbVRlHfHA== 819508855 4
# > ...

This is an example for running the binary:

./gen LGb6W/RZCz9KKw== 2223635746 1
# DfwI12HrGw

Solution⌗

Reversing? Not for me⌗

Since I am the challenge author, I will simply skip the reversing part and paste the source code here. You are the ones who don't have the source code, so good luck to you!

// ...

unsigned int getrand(unsigned int *state) {
    *state = 0x1337 * *state + 0x5;
    return *state;
}

int main (int argc, char **argv) {
    init();
    
    if (argc < 4) {
        printf("Usage: %s <ciphertext> <seed> <rounds>\n", argv[0]);
        exit(-1);
    }

    char state[N]; // N = 100000
    memset(state, 0, sizeof state);

    char *ciphertext = argv[1];
    unsigned int seed = atoi(argv[2]);
    unsigned int rounds = atoi(argv[3]);
    
    char *raw_ciphertext; int outlen;
    raw_ciphertext = base64_decode(ciphertext, strlen(ciphertext), &outlen);

    for (int i = 0; raw_ciphertext[i]; i++) {
        for (int j = 0; j < rounds; j++) {
            unsigned int x = getrand(&seed) % N;
            unsigned int y = getrand(&seed) % N;
            unsigned int z = getrand(&seed);
            if (x > y) x ^= y ^= x ^= y;
            for (int k = x; k < y; k++) state[k] += z;
        }

        unsigned int x = getrand(&seed) % N;
        unsigned int y = getrand(&seed) % N;
        if (x > y) x ^= y ^= x ^= y;
        unsigned char q = 0;
        for (int k = x; k < y; k++) q += state[k];
        printf("%c", raw_ciphertext[i] ^ q);
        fflush(stdout);
    }
    printf("\n");

    return 0;
}

Understanding the code⌗

Suppose that we have a state $S = (s_0, s_1, ..., s_{m-1})$. Define two operations $\text{Update}(l, r, x)$ and $\text{Query}(l, r)$.

• $\text{Update}(l, r, x)$ updates $s_k \leftarrow (s_k + x)\ \text{mod}\ 256$ every $l \leq k < r$.
• $\text{Query}(l, r)$ returns $\left(\sum_{k = l}^{r-1} s_k\right) \text{mod}\ 256$.

With the operations defined, let me update the main function to elaborate.

int main (int argc, char **argv) {
    // ...

    for (int i = 0; raw_ciphertext[i]; i++) {
        for (int j = 0; j < rounds; j++) {
            /*
             * Update(l, r, x)
             */
            unsigned int l = getrand(&seed) % N;
            unsigned int r = getrand(&seed) % N;
            unsigned int x = getrand(&seed);
            // swap l and r if l > r
            if (l > r) l ^= r ^= l ^= r;
            for (int k = x; k < y; k++) state[k] += z;
        }

        /*
         * q := Query(l, r)
         */
        unsigned int l = getrand(&seed) % N;
        unsigned int r = getrand(&seed) % N;
        if (l > r) l ^= r ^= l ^= r;
        unsigned char q = 0;
        for (int k = x; k < y; k++) q += state[k];

        printf("%c", raw_ciphertext[i] ^ q);
        fflush(stdout);
    }
    printf("\n");

    // ...
}

To print one character, $n$ range updates and one range query are performed. The time complexities for $\text{Update}(l, r, x)$ and $\text{Query}(l, r)$ in the binary are both $\mathcal{O}(m)$, which makes the overall complexity to print one character being $\mathcal{O}(km)$. Since $k = 10^4$ in the 100th command, the binary isn't optimized for the challenge.

Data structures can help⌗

I will be skipping the details since this kind of problem is rather common in competitive programming. It is called range sum query (RSQ) and there are multiple data structures those efficiently perform $\text{Update}(l, r, x)$, and optionally $\text{Query}(l, r)$.

For example, segment tree³ can do both in $\mathcal{O}(\log n)$. I would prefer Fenwick tree⁴ (as known as binary indexed tree) because it is the easiest to implement, while maintaining the time complexities for both operations to be $\mathcal{O}(\log n)$. Implementing a Fenwick tree isn't difficult - try it if you didn't!

RC4 (Misc)⌗

Three (out of six) teams have solved this during the CTF period.

Challenge Summary⌗

The Firebird admins do not want too much crypto challenges, so I am going to label this as a misc challenge. But no worries, you can get part of the flag if you achieve something.

nc HOST PORT

Attachments: chall.py, rc4.py

Basically we have an netcat service that sends us a 16-byte key $k_1$. The objective is to send another key $k_2$ such that $\text{RC4}_{k_1}(\text{flag}) = \text{RC4}_{k_2}(\text{flag})$. Also, $k_1$ should not be a substring of $k_2$.

Solution⌗

Is it really a misc-ategorized?⌗

To begin, let's read chall.py.

import sys
import string
import random

from rc4 import RC4
from secret import flag


def prefix_length(u, v):
    for i in range(len(u)):
        if u[i] == v[i]: continue
        return i
    else:
        return len(u)

def convert_key(s):
    return [ord(c) for c in s]

def encrypt(cipher, message):
    return ''.join([chr(ord(message[i]) ^ next(cipher)) for i in range(len(message))])

def main():
    charset = string.ascii_letters + string.digits
    key1 = ''.join(random.choices(charset, k=16))    
    print('🔑', key1)

    key2 = input('🔑 ')

    if key1 in key2:
        print('🤨')
        sys.exit(0)

    key1 = convert_key(key1)
    key2 = convert_key(key2)

    cipher1 = RC4(key1)
    cipher2 = RC4(key2)

    ciphertext1 = encrypt(cipher1, flag)
    ciphertext2 = encrypt(cipher2, flag)
    l = prefix_length(ciphertext1, ciphertext2)

    if l == 0:
        print('🤨')
        sys.exit(0)
    elif l != len(flag):
        print(f'🏁 {flag[:l]}...')
    else:
        print(f'🏁 {flag[:l]}')

if __name__ == '__main__':
    main()

Also, the imported RC4 is copied from the repository bozhu/RC4-Python and slightly updated to make it compatible for Python 3.

This looks evident to find a pair of keys such that the prefixes of the keystream would be identical. There are research⁵⁶ those tried to find pairs of RC4 keys such that the initial states would be the same. In this way, the resulting ciphertext would be identical. This might be an approach, but this would imply that this should not be a misc challenge. Is this my intention? If this is really a crypto challenge, those Firebird guys would hate me for even longer.

The pytfall - Python 2 vs Python 3⌗

Let's cut the crap. Look at how the initial state is generated.

# Lines 16-17, chall.py
def convert_key(s):
    return [ord(c) for c in s]

# Lines 23-34, rc4.py
def KSA(key):
    keylength = len(key)

    # In Python 3, `range` returns an iterator instead of a list...
    S = list(range(256))

    j = 0
    for i in range(256):
        j = (j + S[i] + key[i % keylength]) % 256
        S[i], S[j] = S[j], S[i]  # swap

    return S

Pretty standard. There are implementations online in Python which use a string as the key and perform key-scheduling. For example, manojpandey/rc4, gist from cdleary.

The pseudocode from Wikipedia has showed that the KSA itself is fine. However, since I am writing in Python 3, I should be using bytes instead of str. This is not only a matter of the coding style, but the pitfall, too! Of course, we would not be able to run the above script in Python 2, since f-string is supported since Python 3.6. And even if it is possible, we can simply exploit the program with input. But if we have patched input to raw_input and fixed the compatibility issues, it is likely to be unexploitable. So what's the deal with this? Look at this:

# Python 2
>>> s = raw_input()
🤷
>>> list(map(ord, s))
[240, 159, 164, 183]

# Python 3
>>> s = input()
🤷
>>> list(map(ord, s))
[129335]

This is the documentation for ord in Python 2.7.18⁷:

Given a string of length one, return an integer representing the Unicode code point of the character when the argument is a unicode object, or the value of the byte when the argument is an 8-bit string. For example, ord('a') returns the integer 97, ord(u'\u2020') returns 8224. This is the inverse of chr() for 8-bit strings and of unichr() for unicode objects. If a unicode argument is given and Python was built with UCS2 Unicode, then the character’s code point must be in the range [0..65535] inclusive; otherwise the string length is two, and a TypeError will be raised.

and for Python 3.9⁸:

Given a string representing one Unicode character, return an integer representing the Unicode code point of that character. For example, ord('a') returns the integer 97 and ord('€') (Euro sign) returns 8364. This is the inverse of chr().

That said, the ord function supports unicode characters as default in Python 3. Owing to this, the entries key is not confined in 0 and 255. Hence, knowing this, we can easily win the flag.

$ nc HOST PORT
# 🔑 sRlXr6fBOMPwxlUC
# 🔑 sRlXr6fBOMPwxlUŃ
# 🏁 firebird{n0w_rc4_i5_t0t4lly_4_r3d_h3rr1n9}

Now are you convinced that this is actually a misc challenge? Say yes.

A story behind⌗

This challenge was actually inspired by the unintended solution for OV from De1CTF2020. One day I was messing around with something else and found that chr actually supports a larger set of values (from $[0, 255]$ Python 2 to $[0, 1114111]$ in Python 3). Originally, the challenge would be an exact copy OV and make it work for Sage 9 over Python 3. Unfortunately fetch_int checks the range of the input and someone may smell that easily if I am wiring something else.

Thanks Vergissmeinnichtz for enlightening me for this challenge. You all know who to hate now.