Firebird Internal CTF 2022 Writeup

This is the time that Firebird Internal CTF happens. I made three crypto challenges this year - Lack of Entropy (⭐), Authenticator (⭐⭐) and Collider (⭐⭐). I will discuss the solution for all of them in the blog post.

Lack of Entropy (Crypto)⌗

Three (out of six) teams solved this during the CTF.

Challenge Summary⌗

Mystiz's computer is lack of entropy. He needs to reuse randomness to generate the primes for RSA...

Attachments: chall.py, output.txt

We are given a RSA public key $(n, e)$ and an encrypted flag $c$:

n = 12189464288007059657184858632825479990912616419482466046617619319388181010121359489739982536798361842485210016303524715395474637570227926791570158634811951043352789232959763417380155972853016696908995809240738171081946517881643416715486249
e = 65537
c = 10093874086170276546167955043813453195412484673031739173390677430603113063707524122014352886564777373620029541666833142412009063988439640569778321681605225404251519582850624600712844557011512775502356036366115295154408488005375252950048742

Note that the prime factors of $n$ (namely $p$ and $q$) are generated such that:

\[\begin{cases} p = a_0 + 3 a_1 + 3^2 a_2 + ... \\ q = a_0 + 10 a_1 + 10^2 a_2 + ... \end{cases},\]

where $a_i \in \{0, 1, 2\}$. The objective is to recover the flag.

Solution⌗

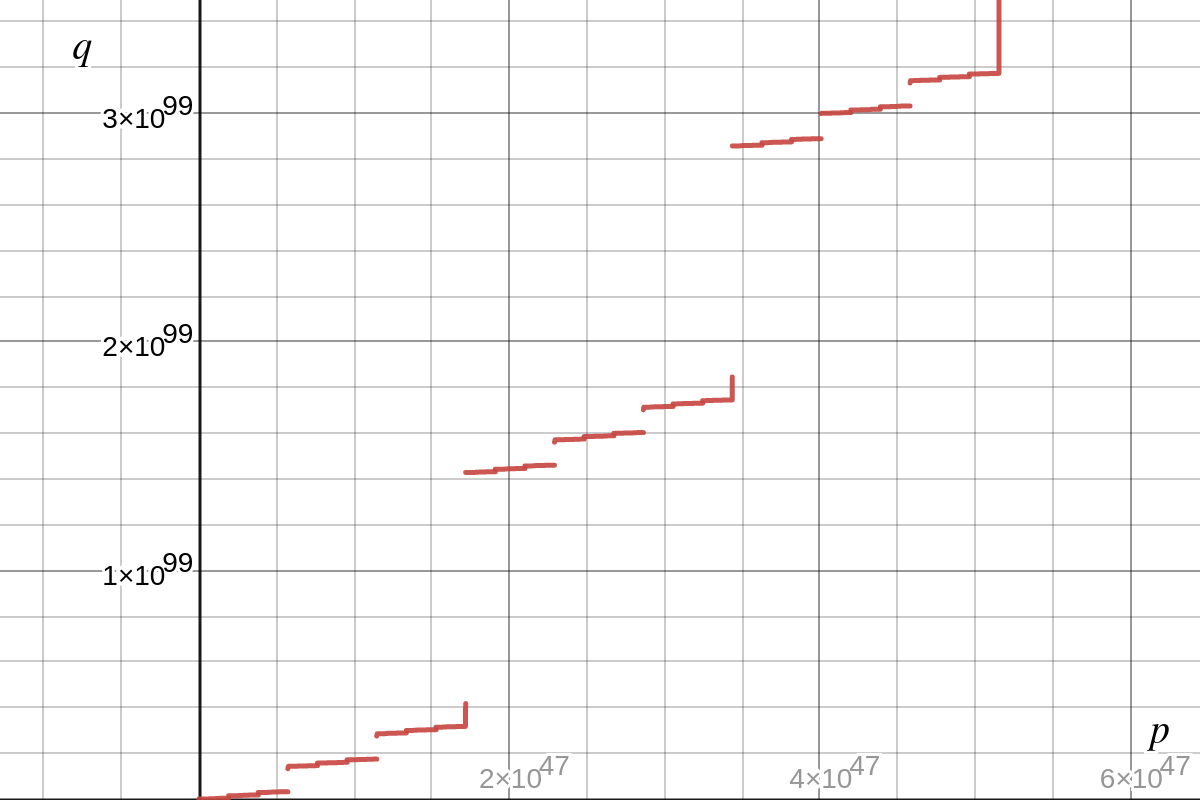
One important fact that we could observe is $q$ increases as $p$ increases (Refer to the above figure). That said, $n = p \cdot q$ also increases as $p$ increases. In that way, we can simply perform binary search on $\tilde{p}$ and check if the corresponding $\tilde{n}$ satisfying:

1. $\tilde{n} < n$ (which imply that $\tilde{p} < p$), or
2. $\tilde{n} > n$ (which imply that $\tilde{p} > p$), or
3. $\tilde{n} = n$ (which imply that $\tilde{p} = p$).

Authenticator (Crypto)⌗

One (out of six) team solved this during the CTF.

Challenge Summary⌗

Hash-based authentication is great and I have invented one. Can you prove that my system is secure?

nc HOST PORT

Attachments: chall.py

Define a protocol $\mathcal{P}$ that is used to authenticates between a client and a server. Suppose that they have a pre-shared password password:

1. Client generates a 16-byte challenge_client and sends it to the server.
2. Server computes the response response_server (specified below) and generates a 16-byte challenge_server.
3. Server sends response_server and challenge_server to the client.
4. Client verifies response_server and aborts if it is incorrect. Otherwise, it computes the response response_client (specified below).
5. Client sends response_client to the server.
6. Server verifies response_client and aborts if it is incorrect. Otherwise, it is said that the authentication is completed.

response_server = blake3(password + "HANDSHAKE_FROM_SERVER" + challenge_client)
response_client = blake3(password + "HANDSHAKE_FROM_CLIENT" + challenge_server)

When connected to the remote service, a 6-character password (that matches the regex /^[0-9a-zA-Z]{6}$/) is generated. The player and the remote service respectively act as the client and the server. The objective is to complete the authentication within 10 seconds (while the player does not know the password).

Solution⌗

Walkthrough for rich person only⌗

Let's cater only the rich guys. You can simply connect to the server and send an arbitrary challenge_client (I will use CHALLENGE_CLIENT for simplicity). Upon receiving the response_server, you can exhaust $62^6$ passwords in ten seconds using a 5680-core machine by checking whether:

response_server == blake3(password + "HANDSHAKE_FROM_SERVER" + "CHALLENGE_CLIENT")

You can proceed the authentication. Done! Easy?

What if I am not that rich?⌗

I guess most of us could not find a 5680-core machine easily. Instead of computing everything online, we can precompute the $62^{6}$ outputs of response_server given that the client's challenge being CHALLENGE_CLIENT. Below is the expected time and space taken for precompution.

• Estimated time taken: 15 hours
• Estimated space taken: 1800 GB

You can proceed the authentication. Done! Easy?

...Of course not! Precomputing for 15 hours is time-consuming, and taking up 1800 GB is absurd. Luckily there are two ways to reduce the time and space complexities by sacrificing a third factor.

Optimization 1: Precompute part of the password space⌗

This is still very resource-intensive with the above optimization. Can we precompute only $1/n$ of the password space? The answer is certain. However, the probability of recovering a password is decreased to $1/n$.

Does it hurt? Not really. If we set $n = 64$, it is expected that we can recover one password every 64 times we connect to the server. This largely decrease the required resources.

• Estimated time taken: 15 minutes (⬇ 98.4%)
• Estimated space taken: 28.4 GB (⬇ 98.4%)
• Estimated service connections: 64 (⬆ 6400.0%)

Optimization 2: Store part of the BLAKE3 digest⌗

We can further reduce the space taken by storing 8 bytes of the digest (instead of the whole digest, which is 32 bytes).

As $62^6 / 64 \lt \sqrt{256^{8}}$, it is unlikely that collision exists. We can reduce the space by 75% sacrificing a little bit of accuracy.

• Estimated time taken: 15 minutes (-)
• Estimated space taken: 7.1 GB (⬇ 75%)
• Estimated service connections: 64 (⬆ $\varepsilon$%)

You can proceed the authentication. Done! Easy?

Collider (Crypto)⌗

Zero (out of six) teams solved this during the CTF.

Challenge Summary⌗

Find a collision for my hash algorithm! It is basically military-graded: The output is 256-bit long, and discrete log is hard! I even made it harder such that you don't even have the public parameters!

nc HOST PORT

Attachments: chall.py

Define a hash algorithm below:

def hash(m):
    m = int.from_bytes(b'SECUREHASH_' + m, 'big')
    return pow(g, m, p).to_bytes(256//8, 'big')

Suppose that the server is running the oracle $\mathcal{O}$ that takes a message $m$ (with only lowercase English letters):

1. Computes $h \leftarrow \mathcal{H}(m)$ and sends $h$ to us.
2. If $m \neq \text{pleasegivemetheflag}$ but $h = \mathcal{H}(\text{pleasegivemetheflag})$, sends the flag to us.

When connected to the server, a 256-bit prime $p$ and a 256-bit number $g$ is generated (and not given to us). We are allowed to call the oracle $\mathcal{O}$ for five times. The goal is to obtain the flag.

Solution⌗

Recovering $g$ and $p$⌗

Since we are given only five calls of $\mathcal{O}$ and we need one for getting the flag, it is expected that we could use at most four calls to recover the parameters $g$ and $p$.

To do so, we can obtain $h_1 = \mathcal{H}(\text{a})$, $h_2 = \mathcal{H}(\text{b})$, $h_3 = \mathcal{H}(\text{c})$ and $h_4 = \mathcal{H}(\text{d})$ via $\mathcal{O}$. Thus

\[h_i = g^{256 \cdot m_0 + 96 + i}\ \text{mod}\ p,\]

where $m_0$ is the prefix SECUREHASH_. Since

\[h_1 \cdot h_3 \equiv g^{512 \cdot m_0 + 196} \equiv {h_2}^2\ (\text{mod}\ p) \quad\text{and}\quad h_2 \cdot h_4 \equiv g^{512 \cdot m_0 + 198} \equiv {h_3}^2\ (\text{mod}\ p),\]

we see that $\gcd(h_1 \cdot h_3 - {h_2}^2, h_2 \cdot h_4 - {h_3}^2)$ is a small multiple of $p$. This allows us to obtain $p$ easily. Now we can effectively recover $g$ by

\[g = h_2 \cdot {h_1}^{-1}\ \text{mod}\ p.\]

By the way, although we have recovered $g$ and $p$, we will not use $g$.

Finding a preimage⌗

Fermat's little theorem stated that $a^{p-1} \equiv 1\ (\text{mod}\ p)$ for $\gcd(a, p) = 1$. Equivalently, if $u$ and $v$ are two padded messages (i.e., in the format SECUREHASH_...), then

\[g^u \equiv g^v \ (\text{mod}\ p) \quad \Longleftrightarrow \quad u \equiv v \ (\text{mod}\ (p-1)).\]

The goal is to find a padded message $u$ such that $u \equiv v\ (\text{mod}\ (p-1))$, with $v$ being the padded message SECUREHASH_pleasegivemetheflag.

Let's present the message mathematically. If we write the unpadded message being $\overline{u_{l-1} u_{l-2} ... u_1 u_0}$, then

\[u = 256^l \cdot m_0 + \sum_{i=0}^{l-1} 256^i \cdot u_i\]

Therefore we need to find $(u_0, u_1, ..., u_{l-1}) \in [97, 122]^{l}$ such that

\[256^{l-1} \cdot u_{l-1} + ... + 256 \cdot u_1 + u_0 + (256^l \cdot m_0 - v) \equiv 0 \quad (\text{mod}\ (p-1)).\]

We can solve the modular congruence with Lenstra–Lenstra–Lovász algorithm. LLL tries to find small roots (i.e., each variable is close to zero) so we need to "adjust the center". If we let $x_i = u_i - 109$ for all $i$'s, then $x_i \in [-12, 13]$ which is smaller in magnitude. Now we have

\[\begin{aligned} & 256^{l-1} \cdot x_{l-1} + ... + 256 \cdot x_1 + x_0 \\ & \qquad + [256^l \cdot m_0 + 109 \cdot (256^{l-1} + ... + 256 + 1) - v] \equiv 0 \quad (\text{mod}\ (p-1)). \end{aligned}\]

Let $s = 256^l \cdot m_0 + 109 \cdot (256^{l-1} + ... + 256 + 1) - v$ (i.e., the right hand side), we know that there is an integer $k$ such that:

\[256^{l-1} \cdot x_{l-1} + ... + 256 \cdot x_1 + x_0 + s + k (p - 1) = 0.\]

At this stage, we can construct the matrix $A$ below:

\[A = \left[\begin{matrix} s \cdot W & 1 & 0 & \dots & 0 & 0 \\ 256^{l-1} \cdot W & 0 & 1 & \dots & 0 & 0 \\ \vdots &&& \ddots && \\ 256^1 \cdot W & 0 & 0 & \dots & 1 & 0 \\ 256^0 \cdot W & 0 & 0 & \dots & 0 & 1 \\ (p-1) \cdot W & 0 & 0 & \dots & 0 & 0 \end{matrix}\right]\]

We can see that $\mathbf{t} := \left[\begin{matrix}0 & 1 & x_{l-1} & ... & x_1 & x_0 \end{matrix}\right]$ is a linear combination of the row vectors of $A$, since

\[\begin{aligned} \mathbf{t} = \left[\begin{matrix}0 & 1 & x_{l-1} & \dots & x_1 & x_0 \end{matrix}\right] &= 1 \cdot \left[\begin{matrix}s \cdot W & 1 & 0 & \dots & 0 & 0\end{matrix}\right] \\ & \quad + x_{l-1} \cdot \left[\begin{matrix}256^{l-1} \cdot W & 0 & 1 & \dots & 0 & 0\end{matrix}\right] \\ & \quad + ... \\ & \quad + x_1 \cdot \left[\begin{matrix}256^1 \cdot W & 0 & 0 & \dots & 1 & 0\end{matrix}\right] \\ & \quad + x_0 \cdot \left[\begin{matrix}256^0 \cdot W & 0 & 0 & \dots & 0 & 1\end{matrix}\right] \\ & \quad + k \cdot \left[\begin{matrix}(p-1) \cdot W & 0 & 0 & \dots & 0 & 0\end{matrix}\right]. \end{aligned}\]

More importantly, the coefficients are integers. If $\lVert\mathbf{t}\rVert$ is small (i.e., $\mathbf{t}$ is short), then we can use LLL to recover such a vector. After all, LLL is an lattice reduction algorithm which is intended to find a set spanned by integer coefficients and short vectors. I suggest reading Cousin's blog post on lattice-based cryptography for an in-depth mathematical context.

We have introduced $W$ without any explanation. What is that? It is just a big number to encourage the first entry of the resulting vectors in the basis to be zero. When the first entry of a vector $\mathbf{v}$ is non-zero, then the length of $\mathbf{v}$ would be inevitably big. Since LLL tries to find a set of short vectors, $\mathbf{v}$ is usually not included in the output. Finally, we can increase $l$ until a vector $\left[\begin{matrix}0 & 1 & x_{l-1} & ... & x_1 & x_0 \end{matrix}\right]$ (where $x_i \in [-12, 13]$) is found. It is suggested to try $l \geq 100$ because $\sqrt[100]{2^{256}} \approx 5.897077$, an average magnitude of the elements in the vector.

Solution script⌗

p = int(input('p = '))
g = 1337

def hash(m):
    m = int.from_bytes(b'SECUREHASH_' + m, 'big')
    return int(pow(g, m, p)).to_bytes(256//8, 'big')


# (x0 + 109) + 256 * (x1 + 109) + 256^2 * (x2 + 109) + ... + 256^(k-1) * (x(k-1) + 109) + 256^k * m0 = v (mod p-1)
m0 = int.from_bytes(b'SECUREHASH_', 'big')
v = int.from_bytes(b'SECUREHASH_pleasegivemetheflag', 'big')

for l in range(100, 200):
    print(f'[ ] Trying {l = }...')
    s = int((sum(256**i * 109 for i in range(l)) + 256**l * m0 - v) % (p-1))
    '''
    [s          1      0      0     ... 0] <-- 1
    [256^(k-1)  0      1      0     ... 0] <-- x(k-1)
    [256^(k-2)  0      0      1     ... 0] <-- x(k-2)
    [                       ...          ]     ...
    [256^0      0      0      0     ... 1] <-- x0
    [p-1        0      0      0     ... 0] <-- *
     ↓          ↓      ↓      ↓         ↓
     0          1      x(k-1) x(k-2)    x0
    '''
    weights = [256] + [1 for _ in range(l+1)]

    A = Matrix(l+2, l+2)
    Q = diagonal_matrix(weights)

    # First column
    A[0, 0] = s
    A[l+1, 0] = p-1
    for i in range(l): A[i+1, 0] = 256^(l-1-i)

    # The remaining columns
    for i in range(l+1): A[i, i+1] = 1

    A *= Q
    A = A.LLL()
    A /= Q

    for row in A:
        if row[0] != 0: continue
        if row[1] < 0: row = -row
        if row[1] != 1: continue
        m = row[2:] # centered by 109

        if min(m) < -12: continue
        if max(m) > 12: continue

        m = bytes(109 + mc for mc in row[2:]).decode()
        print(f"[*] '{m}' has the same hash with 'pleasegivemetheflag'")
        assert False, "Collision found!"