MOCSCTF 2023 Postmortem

I prepared three challenges on behalf of @blackb6a for MOCSCTF, which is a 8-hour long CTF happened yesterday. This blogpost serves as the write-up for the three challenges that I wrote.

There are two solves (out of 40 participants) for Three-pass, and zero solves for jav-asr-ipt and Catch-22 Mini.

Three-pass⌗

Challenge Summary⌗

Shamir is a famous cryptographer. He invented the three-pass protocol, so I don’t see it is unsafe.

Attachments: chall.py, output.txt

Let $(n, e_1)$ and $(n, e_2)$ be the RSA public keys of Alice and Bob, where $d_1$ and $d_2$ are their respective private keys. The flag, $m$, is transmitted from Alice to Bob via a three-pass protocol, specified below:

Alice encrypts $m$, i.e., $c_1 := m^{e_1}\ \text{mod}\ n$ and sends it to Bob,
Bob encrypts $c_1$, i.e., $c_2 := {c_1}^{e_2}\ \text{mod}\ n$ and sends it to Alice,
Alice decrypts $c_2$, i.e., $c_3 := {c_2}^{d_1}\ \text{mod}\ n$ and sends it to Bob,
Bob decrypts $c_3$ and obtains the flag.

We have intercepted $c_1$, $c_2$ and $c_3$. The objective is to recover the flag.

n = 10964288917862750817371943000644790354245952753624811184742882075573503291159213275792617289565174542016890536882446152316020614664981464561310177070588847541824015432685005516483258970286016579654507584001942145685835639042544771196025875926934824854654629287406804175169781542930744041035961354498413636479318500015887509695151706774163342176270668595764352803054030180712959407702145232968072095960248622217033412500318802588364053218099740479457499745048733598734525822270979536699859476431259697698977724661051925808662192259594147272928685323228026419764554817739443779978259966996524027223685447697163661582141
e_a = 7850787509111121843704296046292796209765523362760822778441073322435061020720960202570760122216883325800836925397165034377438443919262547805439050014666281823875017212696850811879873382570464494837703959487875345718181692595018804771684090856135860439183994856735097837364198982869125965085926802347005468560464386462672258583800564648667864628707942109097607368504685011961161864010504692066710237072873338338305230789347300824187187203329273552252494078998862280494814565327762466244260365644318201153240217889101138476813458833584425652814637203342017834450974917962290891504378066826883314533426272066008529842659
e_b = 4453987268676227673717138546198543778490256900761885216399493398056068349494658337928641078100794899095850901032758903950680172209634150955381186281328572137323548410693241837784440962944102633978874827798938332394944037503353368648953561717131174637446457475027140019091092814780388647445775628641143448349527427439477564690099543443277709928131151980500888754622299623842491816224578733956512936055767159814756376096327386916365143301608788828874264501835661518243456338370292578817419693818015476586557623659740708608431858063310083629564657171971965399525567277003986302573053057000412895654326773385514407577323
c1 = 635625603722527732406242842327753945350725694571974401488962916610274697646481993610344372428481397325589618737844538706053099675067921762751397619785858707957914817999667697230069995167574307245259456697677215623906029979279072230370958181299051620924365760774594664872675088357135514004300428557363385290172008755962046341521452462577198740003483664903692948347491024627628714880272778802999826100226453863040788568957321338962180604682917073805800695632705757598907639967058123378499630550480712280533714911130683207438745204963799144060687206195796524968658243175519491950409074500917177663168800511171334501803
c2 = 7795281813608171817794892741379735062226556576265028882723464622060019286100732342981451027687820523245444314645382694811723793808174497214300156934179794205555622005157083862445686945032043405320639519697203684857899172411018428771375767426980596031822470310203233833523614211317164419285700300611034139157137457296864576086638001016651797271883268571688978451037356211059045746855900975366642645162497731774792257449712576044309087316579987978439947563661504990736364718671512316976584629358223866771466264690390020136453075012318174610037220780428939084103590144731860113940987394856986607531349399972658436455908
c3 = 7977921283916873018972258656375438636109648078403403856621256960780183659895530492670743805496687518166195286817025982922117207776910469434997789880448174416587980565856067901272107239948266338560630544165615179249646506219882043808647728828971598358249751709624378172857533066558532071073613752930847449500166165240327454355080420431675080444647400925253148611373039389289751613423304374279739869798080453011631508870963029540554868047053218458677269611062574257854538626076547078009591179864813931791542273673139423996224246974845576047905869390859665905099569747606150666678631706721843828247029345061154431341829

Solution⌗

If we write $c_1$, $c_2$ and $c_3$ into a relation of $m$, $e_1$, $e_2$ and $n$, they are:

$$\left\{\begin{aligned} c_1 &= m^{e_1} \ \text{mod}\ n \\ c_2 &= m^{e_1 e_2} \ \text{mod}\ n \\ c_3 &= m^{e_2} \ \text{mod}\ n \end{aligned}\right..$$

In particular, since $\gcd(e_1, e_2) = 1$, we can obtain $x$ and $y$ such that $x e_1 + y e_2 = 1$ using the extended Euclidean algorithm. In that way we can recover $m$ by computing ${c_1}^x {c_3}^y$, because

$${c_1}^x {c_3}^y = m^{e_1 \cdot x} \cdot m^{e_2 \cdot y} = m^{xe_1 + ye_2} = m^1 = m \ \text{mod}\ n.$$

Therefore we have the flag MOCSCTF{h0w_c0u1d_w3_m4k3_4_s3cur3_7hr33_p4s5}.

jav-asr-ipt⌗

Challenge Summary⌗

Mystiz understands that not everyone writes Python. He specifically creates a crypto challenge in Javascript so that you can run on browsers.

Attachments: app.js, output.json

This challenge implements the RSA algorithm in Javascript. In particular, the below snippet is how the 1024-bit primes $p$ and $q$ are generated.

function generatePrime(p0) {
  while (true) {
    let p = p0
    for (let i = 0; i < 1022; i++) {
      if (Math.random() < 0.5) {
        p += BigInt(1 << i)
      }
    }
    // isPrime implements the Miller-Rabin primality test
    // with the 50 smallest primes.
    if (isPrime(p)) return p
  }
}

// Guaranteed that p - q has a large enough difference:
// p = 0b11xxx...xxx and q = 0b10xxx...xxx
const p = generatePrime(BigInt('2') ** BigInt('1023'))
const q = generatePrime(BigInt('2') ** BigInt('1023') + BigInt('2') ** BigInt('1022'))
const n = p * q

Solution⌗

If we look at the generatePrime function, it appears that $p$ is generated by 1022 random bits $x_0, x_1, …, x_{1021}$, and

$$p = 2^{1023} + x_0 + x_1 \cdot 2 + … + x_{1021} \cdot 2^{1021}.$$

Similarly for $q$. It seems to depend on 1022 random bits $y_0, y_1, …, y_{1021}$:

$$q = 2^{1023} + 2^{1022} + y_0 + y_1 \cdot 2 + … + y_{1021} \cdot 2^{1021}.$$

However, this is not the case. Below is a snippet from the JavaScript documentation on the left shift operator:

The left shift (<<) operator shifts the first operand the specified number of bits, modulo 32, to the left…

With that said, when $i \geq 32$, $b_i$ are shifted $i \ \text{mod}\ 32$ bits instead of $i$ bits. Additionally, 1<<31 equals to $-2^{31}$.

For instance, $p$ is still generated by $x_0, x_1, …, x_{1021}$, but

$$\begin{aligned} p &= 2^{1023} - 2^{31} (x_{31} + x_{63} + … + x_{991}) + 2^{30} (x_{30} + x_{62} + … + x_{990}) \\ & \qquad + 2^{29} (x_{29} + x_{61} + … + x_{1021}) + … + (x_0 + x_{32} + … + x_{992}). \end{aligned}$$

Since $x_0, x_1, …, x_{1021}$ are either 0 or 1, we can see that the upper bound of $p$ being

$$\begin{aligned} p &< 2^{1023} - 2^{31} (0 + 0 + … + 0) + 2^{30} (1 + 1 + … + 1) \\ & \qquad + 2^{29} (1 + 1 + … + 1) + … + (1 + 1 + … + 1) \\ & = 2^{1023} + 2^{30} \cdot 31 + 2^{29} \cdot 32 + … + 32 \\ & < 2^{1023} + 2^{30} \cdot 32 + 2^{29} \cdot 32 + … + 32 \\ & < 2^{1023} + 2^{31} \cdot 32 = 2^{1023} + 2^{36}, \end{aligned}$$

and its lower bound being

$$\begin{aligned} p &> 2^{1023} - 2^{31} (1 + 1 + … + 1) + 2^{30} (0 + 0 + … + 0) \\ & \qquad + 2^{29} (0 + 0 + … + 0) + … + (0 + 0 + … + 0) \\ & = 2^{1023} - 2^{31} \cdot 31 > 2^{1023} - 2^{31} \cdot 32 = 2^{1023} - 2^{36}. \end{aligned}$$

Thus we have $2^{1023} - 2^{36} < p < 2^{1023} + 2^{36}$. Similarly $3 \cdot 2^{1022} - 2^{36} < q < 3 \cdot 2^{1022} + 2^{36}$. We can obtain $p$ by exhausting the values in $(2^{1023} - 2^{36}, 2^{1023} + 2^{36})$ and check if it is a factor of $n$.

Recover $p$ and $q$ mathematically⌗

This is an alternate solution apart from the brute-force approach.

Let $-2^{36} < \Delta p, \Delta q < 2^{36}$ such that

$$\left\{\begin{aligned} p &= 2^{1023} + \Delta p \\ q &= 3 \cdot 2^{1022} + \Delta q \end{aligned}\right.$$

Then $n = pq = (2^{1023} + \Delta p)(3 \cdot 2^{1022} + \Delta q) = 6 \cdot 2^{2044} + 2^{1022} \cdot (3 \Delta p + 2 \Delta q) + \Delta p \cdot \Delta q$.

We can compute $n\ \text{mod}\ 2^{1022}$ to obtain $\Delta p \cdot \Delta q$. With that, we can deduce $3 \Delta p + 2 \Delta q$ as

$$3 \Delta p + 2 \Delta q = (n - 6 \cdot 2^{2044} - \Delta p \cdot \Delta q) / 2^{1022}.$$

Let $v := \Delta p \cdot \Delta q$ and $u := 3 \Delta p + 2 \Delta q$ be the values we obtained. We can combine both relations as a quadratic equation in $\Delta p$:

$$- 3 \Delta p^2 + u \cdot \Delta p - 2v = 0.$$

By solving the quadratic equation, we can obtain $\Delta p$ and is able to factor $n$.

p = 0x8000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000068b26bb1
q = 0xc0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001772381d5

After that, we can compute the private key $d$ and obtain the flag:

MOCSCTF{why_d0_w3_t4ke_m0d_32_to_th3_s3c0nd_op3r4nd}

Catch-22 Mini⌗

Challenge Summary⌗

You need a key to open the door… but what if the key is in the room?

By the way, if you find this challenge similar to HKCERT CTF 2022’s “Catch-22”, it is. I literally plagarized that, except that:

I used CBC instead of ECB to encrypt the token, and

I made the map a little bit smaller, and

I changed the category from crypto to misc,

I refacted the code a little bit to make the logic clearer.

Not a solution: https://hackmd.io/@blackb6a/hkcert-ctf-2022-ii-en-6a196795

By the way, if you want the source code for Catch-22, there you go: https://github.com/samueltangz/ctf-archive-created/tree/master/20221111-hkcert-ctf/catch-22/public

http://HOST:PORT/

Attachments: source.zip

We are given another web game. The player can navigate in the map and the goal is to access the flag.

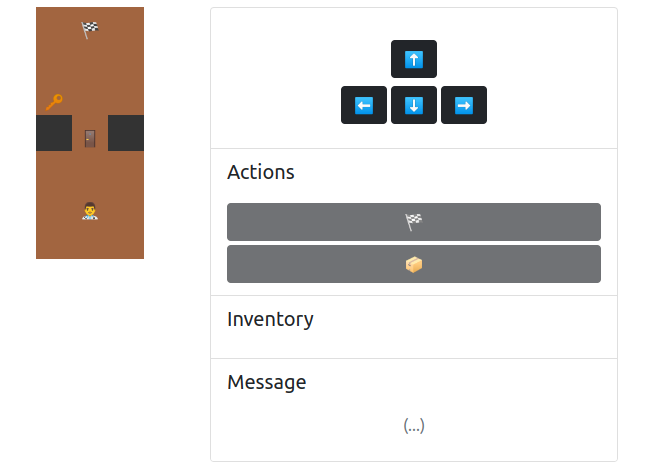
Solution⌗

🎉 Credits. Thanks @LifeIsHard for testing the challenge and giving comments before it is released.

Comparing Catch-22 and Catch-22 Mini⌗

Since Catch-22 is similar to Catch-22 Mini, let’s look at the code and see the diff betwen the two challenges:

  /* src/app.js */

      const newToken = encryptToken({
        username,
-       x: 13,
-       y: 5,
+       x: 5,
+       y: 1,
        inventory: [],
        onMapItems: [
-         {item: ITEMS.KEY, x: 3, y: 4},
-         {item: ITEMS.DOOR, x: 4, y: 5},
-         {item: ITEMS.DOOR, x: 5, y: 5},
-         {item: ITEMS.DOOR, x: 6, y: 5},
-         {item: ITEMS.KEY, x: 15, y: 1},
+         {item: ITEMS.KEY, x: 2, y: 0},
+         {item: ITEMS.DOOR, x: 3, y: 1}
        ]
      })

  /* src/actions.js */

  function isWalkable (x, y, state) {
    // You should not walk out of bounds
    if (x < 0 || x >= MAP.length) return false
    if (y < 0 || y >= MAP[x].length) return false

    // You should not walk more than one blocks away
    if (Math.abs(state.x - x) + Math.abs(state.y - y) != 1) return false
    
    // You should not walk if there is a door blocking
    if (state.onMapItems.find(item => item.x === x && item.y === y && item.item === ITEMS.DOOR)) return false

-   return [TILES.PATH, TILES.PATH_WITH_FLAG].includes(MAP[x][y])
+   // Update by Mystiz at (2022.12.27): Use "not wall" to determine for simplicity.
+   // return [TILES.PATH, TILES.PATH_WITH_FLAG].includes(MAP[x][y])
+   return ![TILES.WALL].includes(MAP[x][y])
  }

  /* src/constants.js */

  const MAP = [
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.PATH, TILES.PATH_WITH_FLAG, TILES.PATH, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.PATH, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.PATH, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.PATH, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.PATH, TILES.WALL],
-   [TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL, TILES.WALL],
+   [TILES.PATH, TILES.PATH_WITH_FLAG, TILES.PATH],
+   [TILES.PATH, TILES.PATH, TILES.PATH],
+   [TILES.PATH, TILES.PATH, TILES.PATH],
+   [TILES.WALL, TILES.PATH, TILES.WALL],
+   [TILES.PATH, TILES.PATH, TILES.PATH],
+   [TILES.PATH, TILES.PATH, TILES.PATH],
+   [TILES.PATH, TILES.PATH, TILES.PATH],
  ]

  /* src/util.js */

  function encryptToken (state) {
    const token = JSON.stringify(state)
-   const cipher = crypto.createCipheriv('aes-128-ecb', key, null)
+   const cipher = crypto.createCipheriv('aes-128-cbc', key, Buffer.alloc(16))
    cipher.setAutoPadding(true)
    const encryptedToken = Buffer.concat([
+     Buffer.alloc(16),
      cipher.update(token),
      cipher.final()
    ])
    return encryptedToken.toString('hex')
  }

  function decryptToken (encryptedTokenHex) {
    const encryptedToken = Buffer.from(encryptedTokenHex, 'hex')
-   const cipher = crypto.createDecipheriv('aes-128-ecb', key, null)
+   const cipher = crypto.createDecipheriv('aes-128-cbc', key, encryptedToken.slice(0, 16))
    cipher.setAutoPadding(true)
    const token = Buffer.concat([
-     cipher.update(encryptedToken),
+     cipher.update(encryptedToken.slice(16)),
      cipher.final()
    ]).toString()
    const state = JSON.parse(token)
    return { token, state }
  }

src/app.js changes the initial position of the player (from $(13, 5)$ to $(5, 1)$) and updated the items on the map (removed one key and two doors).
src/actions.js replaces the isWalkable logic by using a blocklist instead of an allowlist.
src/constants.js defines a smaller map in play.
src/util.js uses AES-CBC to encrypt tokens (instead of AES-ECB) to mitigate the cut-and-paste attack.

The mysterious $1 + \varepsilon = 1$⌗

The intended vulnerability this time was introduced by the new isWalkable method:

function isWalkable (x, y, state) {
  // You should not walk out of bounds
  if (x < 0 || x >= MAP.length) return false
  if (y < 0 || y >= MAP[x].length) return false

  // You should not walk more than one blocks away
  if (Math.abs(state.x - x) + Math.abs(state.y - y) != 1) return false
  
  // You should not walk if there is a door blocking
  if (state.onMapItems.find(item => item.x === x && item.y === y && item.item === ITEMS.DOOR)) return false

  // Update by Mystiz at (2022.12.27): Use "not wall" to determine for simplicity.
  // return [TILES.PATH, TILES.PATH_WITH_FLAG].includes(MAP[x][y])
  return ![TILES.WALL].includes(MAP[x][y])
}

Previously in Catch-22, the destination tile was required to be either TILES.PATH or TILES.PATH_WITH_FLAG for the player to walk on. It is changed so that the tile is not TILES.WALL. Although they seemed equivalent, they are not. You can now walk on a tile if it is undefined.

However, how do we walk on an undefined tile? Note that x and y need not to be integers. It is pretty tricky. For instance, if we are at $(5, 1)$, we cannot move to $(4.5, 1.5)$ because MAP[4.5] is undefined. MAP[4.5][1.5] would raise an TypeError, saying that we cannot read properties of undefined.

To make MAP[x][y] undefined, we have to let MAP[x] returning an array first. With that said, x should be an integer and at the same time y should not. At $(4, 0)$, we can move to $(3, 0.0000000000000001)$. Let’s look at the checks one by one:

// x = 3: it falls within 0 <= x < MAP.length = 7.
if (x < 0 || x >= MAP.length) return false

// y = 0.0000000000000001: it falls within 0 <= y < MAP[3].length = 3.
if (y < 0 || x >= MAP[x].length) return false

// |4 - 3| + |0 - 0.0000000000000001| = 1.0000000000000001...
// ❗ should be returning false here?
if (Math.abs(state.x - x) + Math.abs(state.y - y) != 1) return false

// There is no onMapItems having coordinates (3, 0.0000000000000001).
if (state.onMapItems.find(item => item.x === x && item.y === y && item.item === ITEMS.DOOR)) return false

// Since MAP[3][0.0000000000000001] is undefined, it is not equal to TILES.WALL.
return ![TILES.WALL].includes(MAP[x][y])

Let’s have a little experiment on the Javascript console. The second line returns 1 instead of 1.0000000000000001 because Javascript follows IEEE754 for floating point numbers, which has a 53-bit precision:

0 + 0.0000000000000001 // outputs 1e-16
1 + 0.0000000000000001 // outputs 1

With the above property, we can write a Javascript snippet and paste to the console (after the player enters the grid) to grab the flag.

async function move(dx, dy) { await _action({action: 'move', dx, dy}) }
async function pickFlag() { await _action({action: 'pick-flag'}) }

await move(0, -1)                   // (5, 1) -> (5, 0)
await move(-1, 0)                   // (5, 0) -> (4, 0)
await move(-1, 0.0000000000000001)  // (4, 0) -> (3, 0.0000000000000001)
await move(-1, -0.0000000000000001) // (3, 0.0000000000000001) -> (2, 0)
await move(-1, 0)                   // (2, 0) -> (1, 0)
await move(-1, 0)                   // (1, 0) -> (0, 0)
await move(0, 1)                    // (0, 0) -> (0, 1)
await pickFlag()

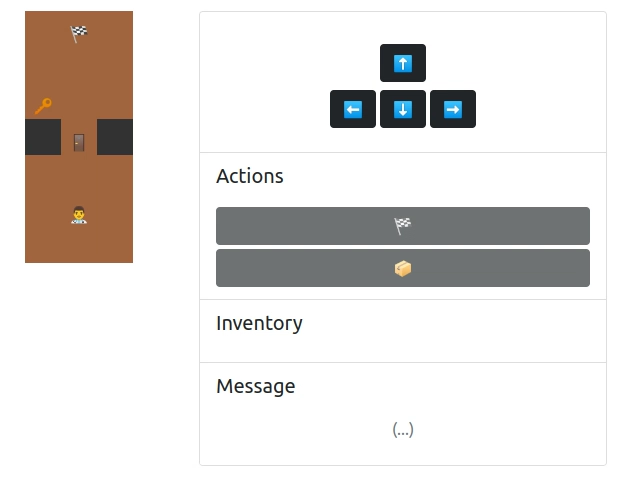
Running the script, we can get the flag MOCSCTF{n0w_y0u_c4n_cl1p_thr0u9h}.