Google CTF 2024 (III): IDEA
Related key attack on reduced-round IDEA
IDEA is a challenge written by @0xdeuterium. He even provided me the paper to refer, my only contribution to the challenge is to optimize the original solution so that we don’t need 65K-ish oracle calls.
Challenge Summary⌗
We have a new idea about a cipher which we think may provide pretty good privacy. So bruce for impact as we may patent our new proposed encryption standard.
nc idea.2024.ctfcompetition.com 1337Attachments: idea.zip
In this challenge, we are asked to break the IDEA cipher with three rounds. We are given 2024 credits, and there are two operations provided by the server:
- Encrypt a given message under the current key (uses 1 credit).
- Flip a bit, specified by the players, of the key (uses 100 credits).
The objective is to recover the original key without using up the credits.
Solution⌗
Background⌗
Section 4.2 of J. Kelsey, B. Schneier, D. Wagner’s paper1 has a brief solution on how to recover the key. Our solution intends to optimize the algorithm by reducing the number of ciphertexts required, as well as the running time by using multiple strategies like meet-in-the-middle.
The below figure shows one round of the IDEA cipher. In our reduced-round scenario, we have $(m_1, m_2, m_3, m_4) = (s_{0, 11}, s_{0, 13}, s_{0, 12}, s_{0, 14})$ and $(c_1, c_2, c_3, c_4) = (s_{4, 1}, s_{4, 2}, s_{4, 3}, s_{4, 4})$ being respectively the plaintext and the ciphertext. Note that for the last round, we have $s_{3, 12} \boxplus k_{4, 2} = c_2$ and $s_{3, 13} \boxplus k_{4, 3} = c_3$ instead of $s_{3, 13} \boxplus k_{4, 2} = c_2$ and $s_{3, 12} \boxplus k_{4, 3} = c_3$.
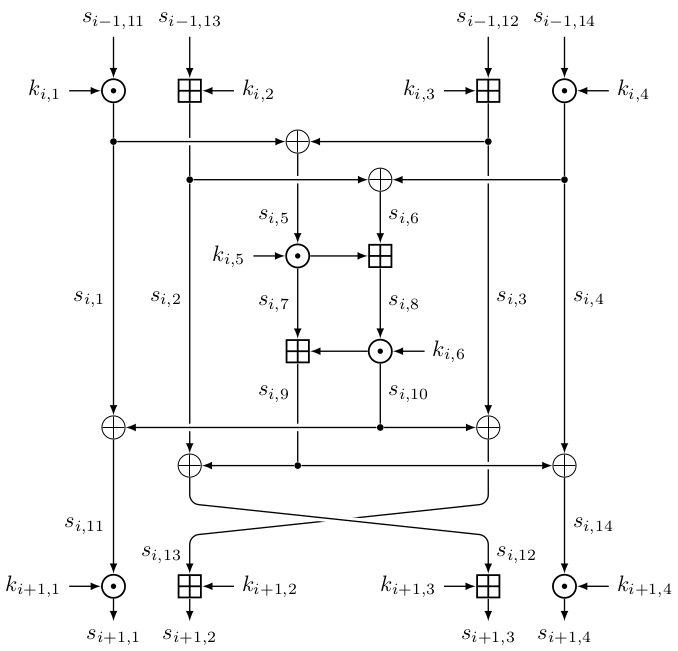
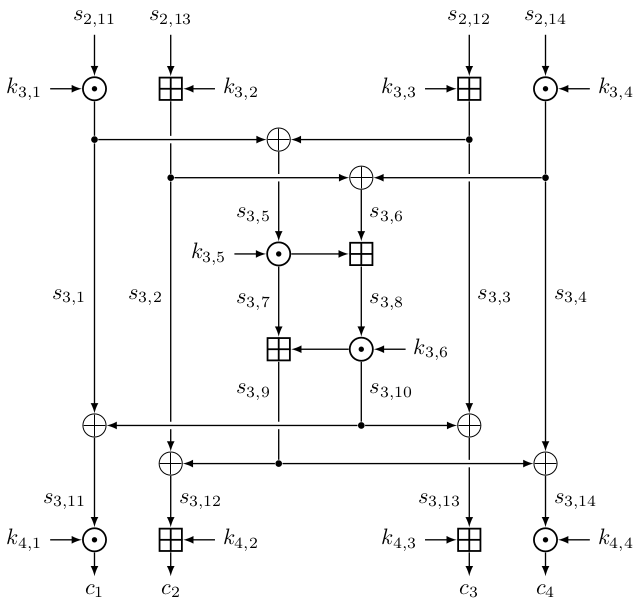
In this writeup, we denote $c^* := \mathcal{E}(K^*, m)$ be the ciphertext of $m$ encrypted with key $K^*$, and $s^*_{i,j}$ as its intermediate values.
The key schedule⌗
IDEA uses a 128-bit key (namely $K$) and its subkeys use a contiguous bit segment. The below table shows the bits used for the subkey $k_{i,j}$. As an example, $k_{1, 1}$ uses bit 127 up to 112, inclusive, which is the top 16 bits of $K$; $k_{4, 3}$ uses the lowest 14 bits of $K$ followed by its top two bits.
| $i$ \ $j$ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 127...112 | 111...96 | 95...80 | 79...64 | 63...48 | 47...32 |
| 2 | 31...16 | 15...0 | 102...87 | 86...71 | 70...55 | 54...39 |
| 3 | 38...23 | 22...7 | 6...119 | 118...103 | 77...62 | 61...46 |
| 4 | 45...30 | 29...14 | 13...126 | 125...110 |
We can view the usage of $K$’s bits. For instance, the most significant bit (bit 127) of $K$ will be used by three subkeys: $k_{1, 1}$, $k_{3, 3}$ and $k_{4, 3}$, bit 109 is only used twice, however, by $k_{1, 2}$ and $k_{3, 4}$.
Step 1: Recovering $k_{4, 1}$ and $k_{4, 3}$ with a bit flip and 4 calls⌗
To recover $k_{4, 1}$ and $k_{4, 3}$, we can compute:
$$ \begin{aligned} & c^{(\text{A}, 1)} := \mathcal{E}(K, (0, 0, 0, 0)), \qquad c^{(\text{B}, 1)} := \mathcal{E}(K', (0, 2^{15}, 0, 0)) \\ & c^{(\text{A}, 2)} := \mathcal{E}(K, (0, 0, 0, 1)), \qquad c^{(\text{B}, 2)} := \mathcal{E}(K', (0, 2^{15}, 0, 1)), \end{aligned} $$
where $K' = K \oplus 2^{111}$. As an example, $c^{(\text{A}, 1)}$ is the ciphertext when we encrypt $(0, 0, 0, 0)$ using the default key.
By flipping bit 111 of the key, only three subkeys would be changed: $k_{1, 2}$, $k_{3, 4}$ and $k_{4, 4}$. In particular, $k'_{1, 2} = k_{1, 2} \oplus 2^{15}$. If we compare the intermediate state for $c^{(\text{A}, i)}$ and $c^{(\text{B}, i)}$, only the values in orange are different:
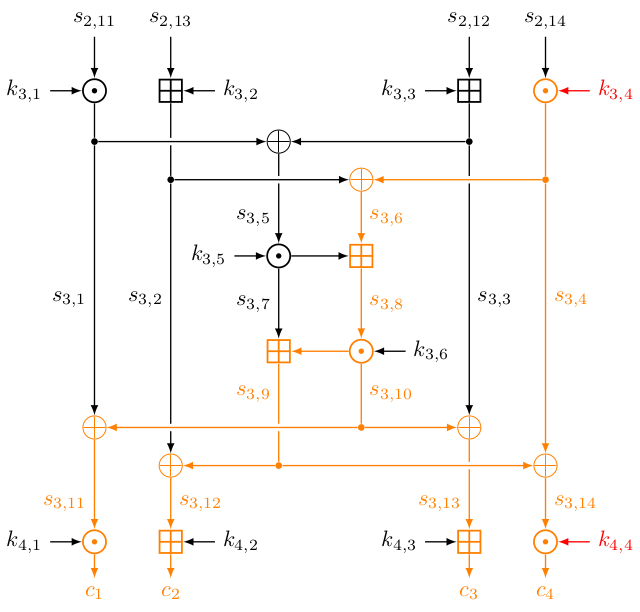
The values that are in black are the same between the two encryptions. For instance, $s^{(\text{A}, i)}_{3, 1} = s^{(\text{B}, i)}_{3, 1}$ and $s^{(\text{A}, i)}_{3, 5} = s^{(\text{B}, i)}_{3, 5}$. In particular, since $s^{(\text{A}, i)}_{3, 5} = s^{(\text{B}, i)}_{3, 5}$, we have
$$ \begin{aligned} & (c^{(\text{A}, i)}_1 \odot k_{4,1}^{-1}) \oplus (c^{(\text{A}, i)}_3 \boxminus k_{4,3}) \\ &\quad = s^{(\text{A}, i)}_{3,11} \oplus s^{(\text{A}, i)}_{3,13} \\ &\quad = (s^{(\text{A}, i)}_{3, 1} \oplus s^{(\text{A}, i)}_{3, 10}) \oplus (s^{(\text{A}, i)}_{3, 10} \oplus s^{(\text{A}, i)}_{3, 3}) \\ &\quad = s^{(\text{A}, i)}_{3, 1} \oplus s^{(\text{A}, i)}_{3, 3} = s^{(\text{A}, i)}_{3, 5} = s^{(\text{B}, i)}_{3, 5} = \dots \\ &\quad = (c^{(\text{B}, i)}_1 \odot k_{4,1}^{-1}) \oplus (c^{(\text{B}, i)}_3 \boxminus k_{4,3}). \end{aligned} $$
Therefore we can exhaust $(k_{4,1}, k_{4,3})$ and check if both of the below equalities hold:
$$ \begin{aligned} & (c^{(\text{A}, 1)}_1 \odot k_{4,1}^{-1}) \oplus (c^{(\text{B}, 1)}_1 \odot k_{4,1}^{-1}) = (c^{(\text{A}, 1)}_3 \boxminus k_{4,3}) \oplus (c^{(\text{B}, 1)}_3 \boxminus k_{4,3}), \\ & (c^{(\text{A}, 2)}_1 \odot k_{4,1}^{-1}) \oplus (c^{(\text{B}, 2)}_1 \odot k_{4,1}^{-1}) = (c^{(\text{A}, 2)}_3 \boxminus k_{4,3}) \oplus (c^{(\text{B}, 2)}_3 \boxminus k_{4,3}) \end{aligned} $$
We can optimize the process with the meet-in-the-middle approach by exhausting the both sides using $k_{4,1}$ and $k_{4,3}$ independently. In this way, we can reduce the time complexity from $\mathcal{O}(2^{32})$ to $\mathcal{O}(2^{16})$:
def step1(rem, candidate_key_list, c1, c2, c3, c4):
new_candidate_key_list = []
c1_1, _, c1_3, _ = c1 # Enc(k, (0x0000, 0x0000, 0x0000, 0x0000))
c2_1, _, c2_3, _ = c2 # Enc(k ^ 2**111, (0x0000, 0x0000, 0x0000, 0x0000))
c3_1, _, c3_3, _ = c3 # Enc(k, (0x0000, 0x0000, 0x0000, 0x0001))
c4_1, _, c4_3, _ = c4 # Enc(k ^ 2**111, (0x0000, 0x0000, 0x0000, 0x0001))
for pk in candidate_key_list:
middletext_to_k41_map = defaultdict(list)
for k41 in pk.subkeys(4, 1):
s1_3_11 = div(c1_1, k41)
s2_3_11 = div(c2_1, k41)
s3_3_11 = div(c3_1, k41)
s4_3_11 = div(c4_1, k41)
middletext = (s1_3_11^s2_3_11, s3_3_11^s4_3_11)
middletext_to_k41_map[middletext].append(k41)
for k43 in pk.subkeys(4, 3):
s1_3_13 = sub(c1_3, k43)
s2_3_13 = sub(c2_3, k43)
s3_3_13 = sub(c3_3, k43)
s4_3_13 = sub(c4_3, k43)
middletext = (s1_3_13^s2_3_13, s3_3_13^s4_3_13)
for k41 in middletext_to_k41_map[middletext]:
new_pk = pk.copy()
new_pk.set_subkey(4, 1, k41)
new_pk.set_subkey(4, 3, k43)
new_candidate_key_list.append(pk)
return new_candidate_key_list
Step 2: Recovering $k_{1, 1}$ with 2 bit flips and 512 calls⌗
Now we want to recover $k_{1, 1}$. To do so, we let $K'' = K \oplus 2^{112}$. Now only $k_{1,1}$, $k_{3,4}$ and $k_{4,4}$ differ and $k''_{1,1} = k_{1,1} \oplus 1$.
Let $c^{(\text{D})}$ and $c^{(\text{E})}$ be ciphertexts encrypted with key $K$ and $K''$, respectively. This time we want to make $s^{(\text{D})}_{1,1} = s^{(\text{E})}_{1,1}$, i.e., $m^{(\text{D})}_1 \odot k_{1,1} = s^{(\text{D})}_{1,1} = s^{(\text{E})}_{1,1} = m^{(\text{E})}_1 \odot (k_{1,1} \oplus 1)$. We do not have a deterministic way to set $m^{(\text{D})}_1$ and $m^{(\text{E})}_1$ because $k_{1,1}$ is unknown. However, we can obtain
$$ c^{(\text{D},i)} := \mathcal{E}(K, (m^{(\text{D})}_{i,1}, 0, 0, 0)) \quad \text{and} \quad c^{(\text{E},j)} := \mathcal{E}(K'', (m^{(\text{E})}_{j,1}, 0, 0, 0)), $$
and check if there exists $i, j$ such that $s_{3,5}^{(\text{D},i)} = s_{3,5}^{(\text{E},j)}$. If that’s the case, we have $[\dagger]$:
$$ m^{(\text{D})}_{i,1} \odot k_{1,1} = m^{(\text{E})}_{j,1} \odot k''_{1,1} = m^{(\text{E})}_{j,1} \odot (k_{1,1} \oplus 1). $$
We then can effectively recover $k_{1,1}$ since we have $m^{(\text{D})}_{i,1}$ and $m^{(\text{E})}_{j,1}$. However, one question remain: How do we pick $m^{(\text{D})}_i$ and $m^{(\text{E})}_j$? The original paper1 suggests us to pick $m^{(\text{D})}_{1,1} = 0$ and $m^{(\text{E})}_{j,1} = j$ for $j = 0, 1, …, 2^{16}-1$, but this requires 65537 oracle calls and we do not have enough credits for that.
Our approach required 512 calls given by $m^{(\text{D})}_i = (5^{-i}, 0, 0, 0)$ for $i = 0, 1, …, 256$ and $m^{(\text{E})}_j = (5^{257j}, 0, 0, 0)$ for $j = 0, 1, …, 254$. Here $a^b$ is given by
$$ a^b = \underbrace{a \odot a \odot \dots \odot a}_{b \ a'\text{s}}. $$
We can substitute the above and rearrange $[\dagger]$ to obtain the below equality:
$$ k_{1,1} \odot (k_{1,1} \oplus 1)^{-1} = 5^{257j + i}. $$
Since $5$ is a primitive root modulo $65537$ and we have $1, 5, 5^2, …, 5^{65534}$ on the right hand side, we are guaranteed that we can find $k_{1,1}$ this way.
Additionally, considering that the two high bits of $k_{1, 1}$ are the two low bits of $k_{4, 3}$, we can filter out some of the keys using the condition (k11>>14) & 0x3 == k43 & 0x3.
def step2(rem, candidate_key_list, c5_list, c6_list):
new_candidate_key_list = []
m5_1_list = [pow(5, -i, 65537) & 0xffff for i in range(257)]
m6_1_list = [pow(5, 257*i, 65537) & 0xffff for i in range(255)]
# solns[x] are the solutions of k such that k / (k^1) = x.
# this could solve k * x1 == (k^1) * x2, where x = x2/x1
solns = [[] for _ in range(65536)]
for k in range(65536):
solns[div(k, k^1)].append(k)
for pk in track(candidate_key_list):
middletext_to_m5_1_map = defaultdict(list)
middletext_to_m6_1_map = defaultdict(list)
k41 = pk.subkey(4, 1)
k43 = pk.subkey(4, 3)
for m5_1, c5 in zip(m5_1_list, c5_list):
c5_1, _, c5_3, _ = c5 # Enc(k, (m5_1, 0x0000, 0x0000, 0x0000))
s5_3_11 = div(c5_1, k41)
s5_3_13 = sub(c5_3, k43)
middletext = s5_3_11 ^ s5_3_13
middletext_to_m5_1_map[middletext].append(m5_1)
for m6_1, c6 in zip(m6_1_list, c6_list):
c6_1, _, c6_3, _ = c6 # Enc(k, (m6_1, 0x0000, 0x0000, 0x0000))
s6_3_11 = div(c6_1, k41)
s6_3_13 = sub(c6_3, k43)
middletext = s6_3_11 ^ s6_3_13
middletext_to_m6_1_map[middletext].append(m6_1)
for middletext in range(2**16):
for m5_1, m6_1 in itertools.product(middletext_to_m5_1_map[middletext],
middletext_to_m6_1_map[middletext]):
for k11 in solns[div(m6_1, m5_1)]:
new_pk = pk.copy()
if not new_pk.set_subkey(1, 1, k11): continue
new_candidate_key_list.append(new_pk)
return new_candidate_key_list
Step 3: Recovering $k_{4, 2}$ and $k_{4, 4}$ with 2 bit flips and 2* calls⌗
Let $K''' = K \oplus 2^{127}$ this time. This time $k_{1, 1}$, $k_{3, 3}$ and $k_{4, 3}$ will be changed, and in particular $k'''_{1, 1} = k_{1, 1} \oplus 2^{15}$. We encrypt two messages with the flipped key:
$$ \qquad c^{(\text{C}, 1)} := \mathcal{E}(K''', (m^{(\text{C})}_1, 0, 0, 0)) \quad \text{and} \quad c^{(\text{C}, 2)} := \mathcal{E}(K''', (m^{(\text{C})}_1, 0, 0, 1)). $$
Here $m^{(\text{C}, i)}$ is given by $0 \odot k_{1, 1} \odot (k_{1, 1} \oplus 2^{15})^{-1}$, as we then could have
$$ \begin{aligned} & s^{(\text{A}, i)}_{1, 1} = m^{(\text{A}, i)}_1 \odot k_{1, 1} = 0 \odot k_{1, 1} \\ & \quad = \left[0 \odot k_{1, 1} \odot (k_{1, 1} \oplus 2^{15})^{-1}\right] \odot (k_{1, 1} \oplus 2^{15}) \\ & \quad = m^{(\text{C}, i)}_1 \odot (k_{1, 1} \oplus 2^{15}) = s^{(\text{C}, i)}_{1, 1}. \end{aligned} $$
Thus only the orange edges in the below figure will be changed.
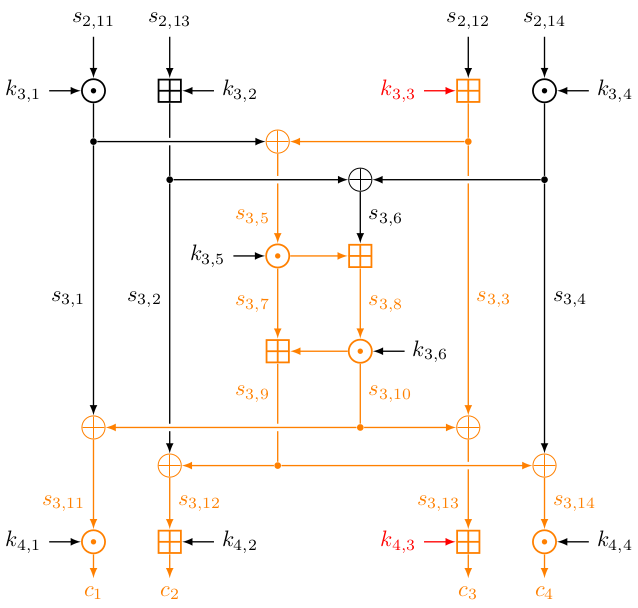
Since $s^{(\text{A}, i)}_{3,6} = s^{(\text{C}, i)}_{3, 6}$, we have
$$ \begin{aligned} & (c^{(\text{A}, i)}_2 \boxminus k_{4,2}) \oplus (c^{(\text{A}, i)}_4 \odot k_{4,4}^{-1}) \\ & \quad = s^{(\text{A}, i)}_{3, 12} \oplus s^{(\text{A}, i)}_{3, 14} = s^{(\text{A}, i)}_{3, 6} = s^{(\text{C}, i)}_{3, 6} = \dots \\ & \quad = (c^{(\text{C}, i)}_2 \boxminus k_{4,2}) \oplus (c^{(\text{C}, i)}_4 \odot k_{4,4}^{-1}). \end{aligned} $$
Hence we can obtain a set of possible $(k_{4, 2}, k_{4, 4})$ using MITM, as what we did in step 1.
def step3(rem, candidate_key_list, c1, c3):
new_candidate_key_list = []
k11_list = set(pk.subkey(1, 1) for pk in candidate_key_list)
rem.switch_key(1<<112 | 1<<127)
k11_to_c7_map = defaultdict(None)
k11_to_c8_map = defaultdict(None)
for k11 in k11_list:
m7_1 = div(mul(k11, 0), k11 ^ (1<<15))
k11_to_c7_map[k11] = rem.enc(m7_1<<48) # Enc(k, (m71, 0x0000, 0x0000, 0x0000))
k11_to_c8_map[k11] = rem.enc(m7_1<<48 | 1) # Enc(k, (m71, 0x0000, 0x0000, 0x0001))
for pk in candidate_key_list:
k11 = pk.subkey(1, 1)
k42_list = pk.subkeys(4, 2)
k44_list = pk.subkeys(4, 4)
c7, c8 = k11_to_c7_map[k11], k11_to_c8_map[k11]
_, c1_2, _, c1_4 = c1
_, c3_2, _, c3_4 = c3
_, c7_2, _, c7_4 = c7
_, c8_2, _, c8_4 = c8
middletext_to_k42_map = defaultdict(list)
for k42 in k42_list:
s1_3_12 = sub(c1_2, k42)
s3_3_12 = sub(c3_2, k42)
s7_3_12 = sub(c7_2, k42)
s8_3_12 = sub(c8_2, k42)
middletext = (s1_3_12^s7_3_12, s3_3_12^s8_3_12)
middletext_to_k42_map[middletext].append(k42)
for k44 in k44_list:
s1_3_14 = div(c1_4, k44)
s3_3_14 = div(c3_4, k44)
s7_3_14 = div(c7_4, k44)
s8_3_14 = div(c8_4, k44)
middletext = (s1_3_14^s7_3_14, s3_3_14^s8_3_14)
for k42 in middletext_to_k42_map[middletext]:
new_pk = pk.copy()
if not new_pk.set_subkey(4, 2, k42): continue
if not new_pk.set_subkey(4, 4, k44): continue
new_candidate_key_list.append(new_pk)
return new_candidate_key_list
Step 4: Recovering $k_{3, 5}$ and $k_{3, 6}$⌗
In this step, we will make use of $c^{(\text{A}, 1)}, c^{(\text{B}, 1)}, c^{(\text{A}, 2)}$ and $c^{(\text{B}, 2)}$ again.
Knowing $k_{4, 1}, k_{4, 2}, k_{4, 3}$ and $k_{4, 4}$, we can retrieve $s_{3, 5}$ and $s_{3, 6}$ by
$$ \begin{aligned} & s_{3, 5} = s_{3, 11} \oplus s_{3, 13} = (c_1 \odot k_{4, 1}^{-1}) \oplus (c_3 \boxminus k_{4, 3}) \\ & s_{3, 6} = s_{3, 12} \oplus s_{3, 14} = (c_2 \boxminus k_{4, 2}) \oplus (c_4 \odot k_{4, 4}^{-1}) \end{aligned} $$
We also know that $s^{(\text{A}, i)}_{3, 1} = s^{(\text{B}, i)}_{3, 1}$ for $i = 1, 2$. We can unveil $s_{3, 1}$ if we have $k_{3, 5}$ and $k_{3, 6}$:
$$ \begin{aligned} & s_{3, 7} = s_{3, 5} \odot k_{3, 5} \\ & s_{3, 8} = s_{3, 6} \boxplus s_{3, 7} \\ & s_{3, 10} = s_{3, 8} \odot k_{3, 6} \\ & s_{3, 1} = s_{3, 10} \oplus s_{3, 11} \end{aligned} $$
We will only accept those $(k_{3, 5}, k_{3, 6})$s such that
$$ s^{(\text{A}, 1)}_{3, 1} = s^{(\text{B}, 1)}_{3, 1} \quad \text{and} \quad s^{(\text{A}, 2)}_{3, 1} = s^{(\text{B}, 2)}_{3, 1}. $$
The above computation required $\mathcal{O}(2^{32})$ and can be optimized. Instead of exhausting $(k_{3, 5}, k_{3, 6})$, we can search for $(s^{(\text{A}, 1)}_{3, 7}, s^{(\text{A}, 1)}_{3, 10})$ instead. Please read the step4_subsolve method below for more details.
# Return a list of (x, y)'s such that (x + y) ^ [x + (y ^ a)] = b
@cache
def step4_subsolve(a, b):
solns = []
# Here we use the substitution u = (x + y) ^ b, and
# perform MITM with (b ^ u) - u = y - (y ^ a).
lhs = defaultdict(list)
for u in range(2**16):
lhs[sub(xor(b, u), u)].append(u)
rhs = defaultdict(list)
for y in range(2**16):
rhs[sub(y, xor(y, a))].append(y)
for v in range(2**16):
for u, y in itertools.product(lhs[v], rhs[v]):
x = sub(xor(b, u), y)
solns.append((x, y))
return solns
def step4(rem, candidate_key_list, c1, c2, c3, c4):
new_candidate_key_list = []
c1_1, c1_2, c1_3, c1_4 = c1
c2_1, c2_2, _, c2_4 = c2
c3_1, c3_2, c3_3, c3_4 = c3
c4_1, c4_2, _, c4_4 = c4
for pk in track(candidate_key_list):
k41 = pk.subkey(4, 1)
k42 = pk.subkey(4, 2)
k43 = pk.subkey(4, 3)
k44 = pk.subkey(4, 4)
s1_3_11 = div(c1_1, k41)
s2_3_11 = div(c2_1, k41)
s3_3_11 = div(c3_1, k41)
s4_3_11 = div(c4_1, k41)
s1_3_12 = sub(c1_2, k42)
s2_3_12 = sub(c2_2, k42)
s3_3_12 = sub(c3_2, k42)
s4_3_12 = sub(c4_2, k42)
s1_3_13 = sub(c1_3, k43)
s3_3_13 = sub(c3_3, k43)
s1_3_14 = div(c1_4, k44)
s2_3_14 = div(c2_4, k44 ^ (1<<1))
s3_3_14 = div(c3_4, k44)
s4_3_14 = div(c4_4, k44 ^ (1<<1))
s1_3_5 = xor(s1_3_11, s1_3_13)
s3_3_5 = xor(s3_3_11, s3_3_13)
s1_3_6 = xor(s1_3_12, s1_3_14)
s2_3_6 = xor(s2_3_12, s2_3_14)
s3_3_6 = xor(s3_3_12, s3_3_14)
s4_3_6 = xor(s4_3_12, s4_3_14)
k35_and_k36_list = []
s1_3_7_and_s1_3_10_list = step4_subsolve(s1_3_11^s2_3_11, s1_3_12^s2_3_12)
for s1_3_7, s1_3_10 in s1_3_7_and_s1_3_10_list:
s1_3_8 = add(s1_3_6, s1_3_7)
k35 = div(s1_3_7, s1_3_5)
k36 = div(s1_3_10, s1_3_8)
k35_and_k36_list.append((k35, k36))
for k35, k36 in k35_and_k36_list:
# Check against the first pair
s1_3_7 = mul(s1_3_5, k35)
s2_3_7 = s1_3_7
s1_3_8 = add(s1_3_6, s1_3_7)
s2_3_8 = add(s2_3_6, s2_3_7)
s1_3_10 = mul(s1_3_8, k36)
s2_3_10 = mul(s2_3_8, k36)
s1_3_1 = xor(s1_3_10, s1_3_11)
s2_3_1 = xor(s2_3_10, s2_3_11)
if s1_3_1 != s2_3_1: continue
# Check against the second pair
s3_3_7 = mul(s3_3_5, k35)
s4_3_7 = s3_3_7
s3_3_8 = add(s3_3_6, s3_3_7)
s4_3_8 = add(s4_3_6, s4_3_7)
s3_3_10 = mul(s3_3_8, k36)
s4_3_10 = mul(s4_3_8, k36)
s3_3_1 = xor(s3_3_10, s3_3_11)
s4_3_1 = xor(s4_3_10, s4_3_11)
if s3_3_1 != s4_3_1: continue
new_pk = pk.copy()
if not new_pk.set_subkey(3, 5, k35): continue
if not new_pk.set_subkey(3, 6, k36): continue
new_candidate_key_list.append(new_pk)
return new_candidate_key_list
Step 5: Recovering $k_{3, 4}$⌗
Now we have fully recovered $k_{3, 5}, k_{3, 6}, k_{4, 1}, k_{4, 2}, k_{4, 3}$ and $k_{4, 4}$, we are able to further reduce the number of rounds from 3 to 2. With that said, we are able to retrieve $s_{3, 1}, s_{3, 2}, s_{3, 3}$ and $s_{3, 4}$ given a ciphertext.
To recover $k_{3, 4}$, we will at $c^{(\text{A}, 1)}$ and $c^{(\text{B}, 1)}$ again. We know what $s^{(\text{A}, 1)}_{3, 4}$ and $s^{(\text{B}, 1)}_{3, 4}$ are, as well as $s^{(\text{A}, 1)}_{2, 14} = s^{(\text{B}, 1)}_{2, 14}$. Therefore, we can exhaust $k_{3, 4}$ and look for the cases when the equality holds.
def step5(rem, candidate_key_list, c1, c2):
new_candidate_key_list = []
c1_1, c1_2, c1_3, c1_4 = c1
_, c2_2, _, c2_4 = c2
for pk in candidate_key_list:
k35 = pk.subkey(3, 5)
k36 = pk.subkey(3, 6)
k41 = pk.subkey(4, 1)
k42 = pk.subkey(4, 2)
k43 = pk.subkey(4, 3)
k44 = pk.subkey(4, 4)
s1_3_11 = div(c1_1, k41)
s1_3_12 = sub(c1_2, k42)
s2_3_12 = sub(c2_2, k42)
s1_3_13 = sub(c1_3, k43)
s1_3_14 = div(c1_4, k44)
s2_3_14 = div(c2_4, k44 ^ (1<<1))
s1_3_5 = xor(s1_3_11, s1_3_13)
s2_3_5 = s1_3_5
s1_3_6 = xor(s1_3_12, s1_3_14)
s2_3_6 = xor(s2_3_12, s2_3_14)
s1_3_7 = mul(s1_3_5, k35)
for k34 in pk.subkeys(3, 4):
s1_3_7 = mul(s1_3_5, k35)
s2_3_7 = mul(s2_3_5, k35)
s1_3_8 = add(s1_3_6, s1_3_7)
s2_3_8 = add(s2_3_6, s2_3_7)
s1_3_10 = mul(s1_3_8, k36)
s2_3_10 = mul(s2_3_8, k36)
s1_3_9 = add(s1_3_7, s1_3_10)
s2_3_9 = add(s2_3_7, s2_3_10)
s1_3_4 = xor(s1_3_9, s1_3_14)
s2_3_4 = xor(s2_3_9, s2_3_14)
s1_2_14 = div(s1_3_4, k34)
s2_2_14 = div(s2_3_4, k34 ^ (1<<8))
if s1_2_14 != s2_2_14: continue
new_pk = pk.copy()
new_pk.set_subkey(3, 4, k34)
new_candidate_key_list.append(new_pk)
return new_candidate_key_list
Step 6: Recovering $k_{1, 3}$⌗
We can use $c^{(\text{A}, 1)}$ to recover $k_{1, 3}$ this time. Up to now, only $k_{1, 2}, k_{1, 3}, k_{1, 4}, k_{2, 3}$ and $k_{2, 4}$ are unknown. Fortunately, we still can recover $s^{(\text{A}, 1)}_{1, 3}$ from its ciphertext. With that, we can obtain $k_{1, 3}$ with $k_{1, 3} = s^{(\text{A}, 1)}_{1, 3} \boxminus m^{(\text{A}, 1)}_3 = s^{(\text{A}, 1)}_{1, 3}$.
def step6(rem, candidate_key_list, c1):
new_candidate_key_list = []
m1_1, _, m1_3, _ = 0x0000, 0x0000, 0x0000, 0x0000
c1_1, c1_2, c1_3, c1_4 = c1
for pk in candidate_key_list:
k11 = pk.subkey(1, 1)
k21 = pk.subkey(2, 1)
# omitted for brevity...
k43 = pk.subkey(4, 3)
k44 = pk.subkey(4, 4)
s1_3_11 = div(c1_1, k41)
s1_3_12 = sub(c1_2, k42)
# omitted for brevity...
s1_1_13 = sub(s1_2_2, k22)
s1_1_3 = xor(s1_1_10, s1_1_13)
k13 = sub(s1_1_3, m1_3)
new_pk = pk.copy()
new_pk.set_subkey(1, 3, k13)
new_candidate_key_list.append(new_pk)
return new_candidate_key_list
Step 7: Recovering the entire key!⌗
At this moment, only nine bits of $K$ are unknown. We can simply exhaust the possible keys and check if $(0, 0, 0, 0)$ encrypts to $c^{(\text{A}, 1)}$, as well as $(0, 0, 0, 1)$ encrypts to $c^{(\text{A}, 2)}$. It is very likely that the $K$ recovered is unique. With the key recovered, we can send that to retrieve our flag: CTF{we_have_no_idea_on_related_key_attacks}.
def step7(rem, candidate_key_list, c1, c3):
new_candidate_key_list = []
m1 = 0x0000_0000_0000_0000
m3 = 0x0000_0000_0000_0001
for pk in candidate_key_list:
for key in pk.keys:
cipher = IDEA(key, rounds=3)
if split_chunks(cipher.encrypt(m1)) != c1: continue
if split_chunks(cipher.encrypt(m3)) != c3: continue
new_pk = pk.copy()
if not new_pk.set_key(key): continue
new_candidate_key_list.append(new_pk)
return new_candidate_key_list
-
J. Kelsey, B. Schneier, D. Wagner (2016). “Key-Schedule Cryptanalysis of IDEA, G-DES, GOST, SAFER, and Triple-DES”
https://www.schneier.com/wp-content/uploads/2016/02/paper-key-schedule.pdf ↩︎