HITCON CTF 2024 Writeup

The crypto challenge authors in HITCON 2024, @maple3142 and @_bronson113 prepared a set of exciting and difficult challenges.

I collaborated with @thehackerscrew1 as a guest player this time. In this blog post, we will cover three challenges: ZKPoF, PCBC Revenge and Hyper512.

ZKPoF⌗

Challenge Summary⌗

This challenge implements the proof-of-knowledge protocol for factoring specified in Poupard and Stern’s paper¹, where the server and us take turn being the verifier.

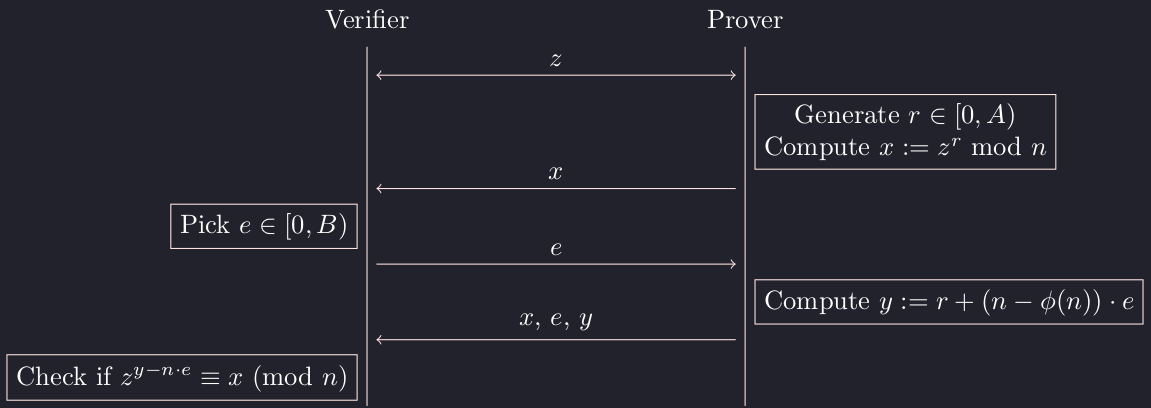
In the challenge, we have $A = 2^{1000}$ and $B = 2^{80}$. We are the verifier and the server is the prover on the first part of the connection. We can ask for up to 311 proofs:

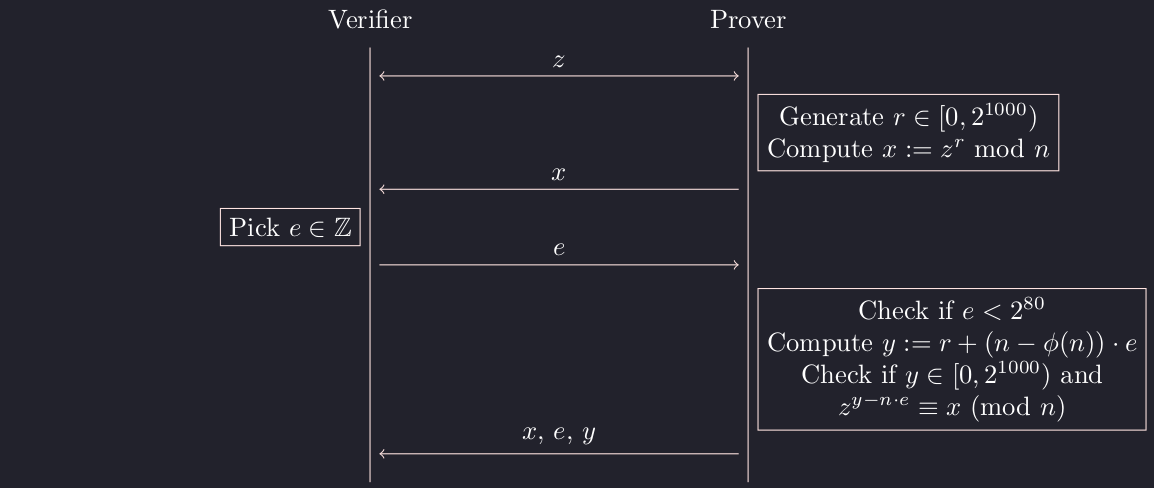
The roles are swapped on the second part. We are asked to construct 13 proofs:

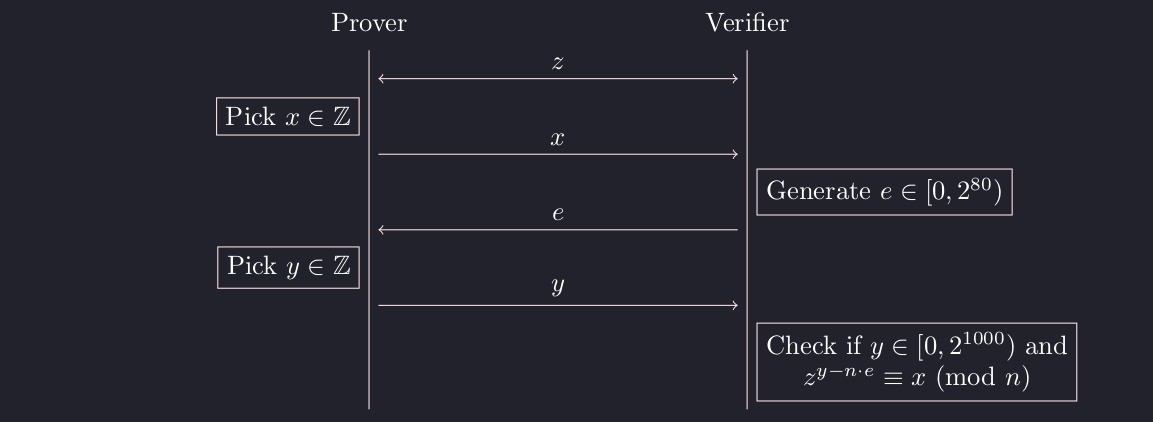
The objective is to successfully construct proofs when we are the prover.

Solution⌗

Part I: Yes Mystiz’s trick⌗

The first thing I see is $e$ can be negative when we are the verifiers… Apparently @maple3142 is not as careful as @Utaha!

def zkpof(z, n, phi):
    # I act as the prover
    r = getRandomRange(0, A)
    x = pow(z, r, n)
    e = int(input("e = "))
    if e >= B: # 👈 WARNING: This can be negative
        raise ValueError("e too large")
    y = r + (n - phi) * e
    transcript = {"x": x, "e": e, "y": y}
    return json.dumps(transcript)

I immediately assumed that we can send $e = -A$, and we can obtain $y = r - (n - \phi) \cdot A$ from the verifier. Since $r \in [0, A)$, we can recover $\phi$ effectively. Let’s go!

Wait no. It runs assert zkpof_verify(z, t, n) before we are given the transcript. Since the $y$ we have is negative, we did not fulfil the condition $0 \le y \lt A$:

def zkpof_verify(z, t, n):
    transcript = json.loads(t)
    x, e, y = [transcript[k] for k in ("x", "e", "y")]
    return 0 <= y < A and pow(z, y - n * e, n) == x

Fortunately, this is not the end of the world. Notably, the server is running Python 3.12, where we will be condemned when a large number like $10^{4300}$ is constructed².

Let’s look again at code snippet that we act as the verifiers:

z = rand.randrange(2, n)
t = zkpof(z, n, phi)
assert zkpof_verify(z, t, n)

There are multiple reasons that the above snippet will lead to an exception, where #1 and #2 come from zkpof, and #3 comes from zkpof_verify:

1. Error: e too large if $e \ge B$.
2. Error: Exceeds the limit (4300 digits)... if $|y| \ge 10^{4300}$.
3. Error: if $y < 0$ or $y \ge A$ or $z^{y - ne} \not\equiv x \ (\text{mod}\ n)$.

Now we can know whether $y < -10^{4300}$ from the server’s response. For instance, we can send $e = -\lceil 10^{4300} / 2^{512} \rceil$ to check whether $\phi \le n - 2^{512}$. We will can leak one bit of $\phi$ using binary search by choosing appropriate $e$s. Since we have 311 oracle calls, we can leak 311 bits of $n - \phi$. Since $n - \phi = p + q - 1 < 2^{513}$, we only have around 200 bits that remained unknown.

Part II: Lattice for the win⌗

Now we have an approximation of $p + q = n - \phi + 1$ (we have 311/513 bits of it), we can estimate $p$ by first computing $p - q = \sqrt{(p + q)^2 - 4n}$ (assuming $p > q$) then obtain

$$ p = \frac{1}{2}(p + q) + \frac{1}{2}(p - q). $$

Now we have an approximated $p$ (namely $\tilde p$), which the error is around 200 bits. Since we have a large portion of $p$, we can recover the rest using LLL. We can use the polynomial $\text{f}(x) = \tilde p + x$ and look for small roots over modulo $n$. With $p$ recovered, we can now construct valid proofs as a prover and convince the server for the flag:

hitcon{the_error_is_leaking_some_knowledge}

PCBC Revenge⌗

Challenge Summary⌗

We are given the $\text{Encrypt}$ function, which is based on a custom mode of operation with three keys, $k_0$, $k_1$ and $k_2$. The implementation is given in the Python snippet below:

def encrypt(message):
    cipher = b""
    prev_block = iv # 👈 "iv" is a constant per connection
    counter1 = counter(nonce1)
    counter2 = counter(nonce2)
    for block in get_blocks(pad(message, BLOCK_SIZE)):
        enc1 = AES_ECB_enc(key_ctr1, next(counter1))
        enc2 = AES_ECB_enc(key_cbc, xor(block, prev_block, enc1))
        enc3 = AES_ECB_enc(key_ctr2, next(counter2))
        # 👆 "key_cbc", "key_ctr1" and "key_ctr2" will be labeled as k0, k1 and k2
        enc4 = xor(enc3, enc2)
        prev_block = xor(block, enc4)
        cipher += enc4

    return iv + cipher

The below figure shows one round of the given mode of operation for $i = 1, 2, …$:

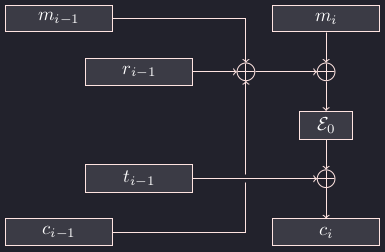
Here $m_0 = \texttt{00 00 … 00}$. Also, for $i = 0, 1, …$, we have

$$r_i = \mathcal{E}_1(\text{nonce}_1 + i) \quad \text{and} \quad t_i = \mathcal{E}_2(\text{nonce}_2 + 1).$$

When connected to the server, we are given the encrypted flag $c_\text{flag}$. We are also given the two functions below, and we can call them as much as we want:

1. [Generate a plaintext-ciphertext pair] We send $0 \le l < 4096$ to the server. The server generates a message $m$ of length $l$ and computes $c = \text{Encrypt}(m)$. We are then given $(m, c)$. Note that the IV remains unchanged throughout the connection.
2. [Padding oracle] We send $c = (c_0, c_1, …, c_n)$ to the server. The server decrypts it and checks if the flag is a substring of $m$, or there is an exception. Note that $c_0$ should be unchanged.

Solution⌗

Part I: Why it is easy when IV can be controlled?⌗

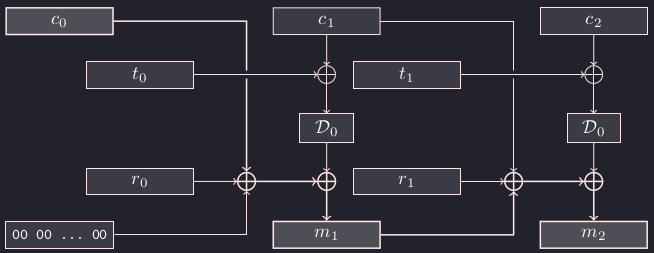
Suppose that a ciphertext for $(m_1, m_2, …, m_n)$ is $(c_0, c_1, …, c_n)$. In the Counter Block Chaining challenge, we were able to control the initialization vector. By changing the IV from $c_0$ to $c'_0$, we have

$$ m_1 \oplus m'_1 = m_2 \oplus m'_2 = … = m_n \oplus m'_n = c_0 \oplus c'_0. $$

With this, we can attack the padding oracle in the same way we do for the CBC mode. For instance, if we want to recover the last byte of $m_n$, we can make the last byte of $c'_0$ to be $\texttt{00}$, $\texttt{01}$, …, $\texttt{FF}$ until $(c_0', c_1, …, c_n)$ corresponds to a plaintext that has a valid PKCS7 padding. In that case, the trailing byte of $m_n'$ will be $\texttt{01}$, thus we can deduce the trailing byte of $m_n$ using $m_n = m'_n \oplus c_0 \oplus c'_0$.

Part II: We cannot control the IV!⌗

In this challenge, we can no longer flip $c_0$ to generate an arbitrary $m_n$ for the padding oracle. To make matters worse, for $i = 1, 2, …, n$, $m_i$ is dependent of $c_i$. We do not have a simple relation like the above.

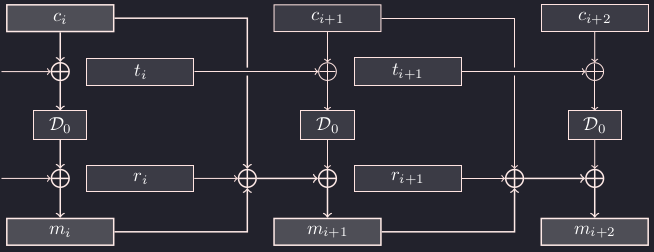
If we change the $i$-th block of the ciphertext from $c_i$ to $c'_i$, we have

$$ \begin{aligned} & m_{i+1} \oplus m'_{i+1} = m_{i+2} \oplus m'_{i+2} = … = m_n \oplus m'_n \\ &\qquad = \mathcal{D}_0(c_i \oplus t_{i-1}) \oplus \mathcal{D}_0(c_i' \oplus t_{i-1}) \oplus c_i \oplus c_i' \\ &\qquad = m_i \oplus m_i' \oplus c_i \oplus c_i'. \end{aligned}$$

Now we want to recover the plaintext $(m_{0,1}, …, m_{0,n})$ from its ciphertext $(c_{0,0}, …, c_{0,n})$. We need two known plaintext-ciphertext pairs that is 129 blocks longer, namely,

$$\begin{aligned} & (m_{1,1}, …, m_{1, n+129}) \xrightarrow{\text{Encrypt}} (c_{1,0}, …, c_{1, n+129}) \\ & (m_{2,1}, …, m_{2, n+129}) \xrightarrow{\text{Encrypt}} (c_{2,0}, …, c_{2, n+129}) \end{aligned}$$

Denote $\Delta_{ij} := m_{1, j} \oplus m_{i, 1} \oplus c_{1, j} \oplus c_{i, j}$ for $i = 1, 2$ and $j = 0, 1, …, n+128$. Additionally, we would want that for any $u \in [0, 2^{128})$, there exists $i_1, …, i_{128} \in \{0, 1\}$ such that

$$\Delta_{i_1, n+1} \oplus \Delta_{i_2, n+2} \oplus … \oplus \Delta_{i_{128}, n+128} = u.$$

We can generate two such plaintext-ciphertext pairs using the first function. Now suppose that we want to recover the last byte of $m_{0, 1}$. We will use

$$(c_{1, 0}, c_{0, 1}, c_{1, 2}, …, c_{1, n}, c_{i_1, n+1}, …, c_{i_{128}, n+128}, c_{1, n+129}).$$

For the ciphertext, its last message block, $\tilde{m}_{n+129}$, would be

$$\begin{aligned} \tilde{m}_{n+129} &= m_{n+129} \oplus \Delta_{0, 1} \oplus \Delta_{i_1, n+1} \oplus … \oplus \Delta_{i_{128}, n+128} \\ &= m_{n+129} \oplus (m_{1, 1} \oplus m_{0, 1} \oplus c_{1, 1} \oplus c_{0, 1}) \oplus \Delta_{i_1, n+1} \oplus … \oplus \Delta_{i_{128}, n+128}. \end{aligned}$$

Rearranging, we have

$$m_{1, 1} = \tilde{m}_{n+129} \oplus m_{n+129} \oplus m_{0, 1} \oplus c_{1, 1} \oplus c_{0, 1} \oplus \Delta_{i_1, n+1} \oplus … \oplus \Delta_{i_{128}, n+128}.$$

The only unknown variables would be $\tilde{m}_{n+129}$ and $m_{0, 1}$. However, if we are sending this ciphertext to the second function, we will be informed if $\tilde{m}_{n+129}$ has a valid PKCS7 padding. Thus we can control $\Delta_{i_1, n+1} \oplus … \oplus \Delta_{i_{128}, n+128}$ by solving a linear system over $\text{GF}(2)$. If $\tilde{m}_{n+129}$ ends with 01 when $\Delta_{i_1, n+1} \oplus … \oplus \Delta_{i_{128}, n+128} = u$, then the padding is valid and we can recover the last byte of $m_{1, 1}$ by looking at the last byte of the above equality.

Repeating the process, we are able to recover the entire flag:

hitcon{just_a_normal_padding_oracle_with_some_linear_algebra..._horray!_1f4614e8211bddb81b05b}

Hyper512⌗

Challenge Summary⌗

We are given the below stream cipher which makes use of four 128-bit LFSRs:

class Cipher:
    def __init__(self, key: int):
        self.lfsr1 = LFSR(128, key, MASK1)
        key >>= 128
        self.lfsr2 = LFSR(128, key, MASK2)
        key >>= 128
        self.lfsr3 = LFSR(128, key, MASK3)
        key >>= 128
        self.lfsr4 = LFSR(128, key, MASK4)

    def bit(self):
        x = self.lfsr1() ^ self.lfsr1() ^ self.lfsr1()
        y = self.lfsr2()
        z = self.lfsr3() ^ self.lfsr3() ^ self.lfsr3() ^ self.lfsr3()
        w = self.lfsr4() ^ self.lfsr4()
        return (
            sha256(str((3 * x + 1 * y + 4 * z + 2 * w + 3142)).encode()).digest()[0] & 1
        )

    def stream(self):
        while True:
            b = 0
            for i in reversed(range(8)):
                b |= self.bit() << i
            yield b

    def encrypt(self, pt: bytes):
        return bytes([x ^ y for x, y in zip(pt, self.stream())])

    def decrypt(self, ct: bytes):
        return self.encrypt(ct)

We are given a ciphertext encrypted with the above Cipher, where its plaintext is 4096 null bytes followed by the flag. The objective is to recover the flag.

Solution⌗

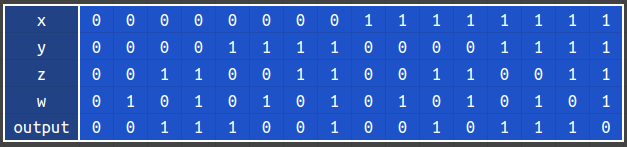
Let $x_i, y_i, z_i, w_i, \text{output}_i$ be the $i$-th bit from lfsr1, lfsr2, lfsr3, lfsr4 and the output. @KLPP observed that if $\text{output}_i = 1$, then $y_i = 1$ or $z_i = 1$. This is equivalent to $(y_i - 1) (z_i - 1) = 0$.

Additionally, we can express $y_i$ (resp. $z_i$) in terms of $y_1, …, y_{128}$ (resp. $z_1, …, z_{128}$) given the masks. Let’s write $y_i = a_{i,1} y_1 + … + a_{i,128} y_{128}$ and $z_i = b_{i,1} z_1 + … + b_{i,128} z_{128}$, and we know those $a_{ij}$ and $b_{ij}$’s.

To reiterate, for each $i$ such that $\text{output}_i = 1$, we have

$$(a_{i,1} y_1 + … + a_{i,128} y_{128} - 1)(b_{i,1} z_1 + … + b_{i,128} z_{128} - 1) = 0.$$

We can expand that and obtain the long equation below:

$$\begin{aligned} & (a_{i,1}b_{i,1} \cdot {\color{red}{y_1z_1}} + … + a_{i,128}b_{i,128} \cdot {\color{red}{y_{128}z_{128}}}) \\ & \qquad + (a_{i,1} \cdot {\color{red}{y_1}} + … + a_{i,128} \cdot {\color{red}y_{128}}) + (b_{i,1} \cdot {\color{red}{z_1}} + … + b_{i,128} \cdot {\color{red}{z_{128}}}) = 1 \end{aligned}$$

We can try to linearize the equation since there will be 16368 such equations given in output.txt (one equation upon $\text{output}_1 = 1$):

$$\begin{aligned} & (a_{i,1}b_{i,1} \cdot {\color{red}{u_1}} + … + a_{i,128}b_{i,128} \cdot {\color{red}{u_{16384}}}) \\ & \qquad + (a_{i,1} \cdot {\color{red}{u_{16385}}} + … + a_{i,128} \cdot {\color{red}u_{16512}}) + (b_{i,1} \cdot {\color{red}{u_{16513}}} + … + b_{i,128} \cdot {\color{red}{u_{16640}}}) = 1 \end{aligned}$$

Now we have 16640 unknowns, we have 272 degrees of freedom. Fortunately, we can pick three $x_i$’s and assume that they are zeroes. This makes all the $u_j$’s depending on the $x_i$’s are zeroes, too. We only need to guess 8 times on average to obtain the correct $u_j$’s (thus $y_1, …, y_{128}$ and $z_1, …, z_{128}$).

Now we have $y_i$ and $z_i$’s. To proceed, we see from the truth table that the only case when $(y_i, z_i, \text{output}_i) = (0, 1, 0)$ is $(x_i, w_i) = (1, 1)$. We can collect 256 such values to recover $x_1, …, x_{128}$ and $w_1, …, w_{128}$. Since the key is fully recovered, we can proceed to retrieve the flag:

hitcon{larger_states_is_still_no_match_of_fast_correlation_attacks!}