Crypto in CTF: Q4 2021
| CTF | Challenge Name | Solves (Difficulty) |
|---|---|---|
| TSG CTF 2021 | Beginner's Crypto 2021 | 126/775 (⭐) |
| TSG CTF 2021 | Minimalist's Private | 49/775 (⭐⭐) |
| TSG CTF 2021 | Baba is Flag | 34/775 (⭐⭐) |
| TSG CTF 2021 | Flag is Win | 10/775 (⭐⭐⭐) |
| TSG CTF 2021 | This is DSA | 9/775 (⭐⭐) |
| TastelessCTF 2021 | crybaby 🔥 | 14/162 (⭐⭐⭐) |
| pbctf 2021 | Alkaloid Stream | 132/210 (⭐⭐) |
| pbctf 2021 | Steroid Stream | 38/210 (⭐⭐) |
| pbctf 2021 | GoodHash 🔥 | 30/210 (⭐⭐⭐) |
| pbctf 2021 | Seed Me 🔥 | 24/210 (⭐⭐⭐) |
| pbctf 2021 | Yet Another PRNG 🔥 | 14/210 (⭐⭐⭐) |
| pbctf 2021 | Yet Another RSA 🔥 | 12/210 (⭐⭐⭐) |
| Hack.lu CTF 2021 | Silver Water Industries | 92/174 (⭐⭐) |
| Hack.lu CTF 2021 | WhatTheHecc | 45/174 (⭐⭐) |
| Hack.lu CTF 2021 | lwsr | 20/174 (⭐⭐) |
| BSides Ahmedabad CTF 2021 | dlppp | 39/314 (⭐⭐) |
| BSides Ahmedabad CTF 2021 | floorsa | 27/314 (⭐⭐) |
| BSides Ahmedabad CTF 2021 | SSSS.RNG 🔥 | 16/314 (⭐⭐) |
| BSides Ahmedabad CTF 2021 | ECC-RSA 2 🔥 | 8/314 (⭐⭐⭐) |
| BSides Ahmedabad CTF 2021 | They Were Eleven 🔥 | 3/314 (⭐⭐⭐⭐) |
| HKCERT CTF 2021 | A Joke Cipher | 88/239 (⭐) |
| HKCERT CTF 2021 | Cipher Mode Picker | 21/239 (⭐) |
| HKCERT CTF 2021 | Key Backup Service 1 | 6/239 (⭐⭐) |
| HKCERT CTF 2021 | Key Backup Service 2 | 5/239 (⭐⭐) |
| HKCERT CTF 2021 | Tenet: The Plagarism | 4/239 (⭐⭐) |
| HKCERT CTF 2021 | Sratslla SEA | 2/239 (⭐⭐⭐) |
| HKCERT CTF 2021 | Sign In Please, Again | 2/239 (⭐⭐⭐) |
| Balsn CTF 2021 | 1337 pins | 5/284 (⭐⭐⭐) |
| Balsn CTF 2021 | dlog 🔥 | 2/284 (⭐⭐⭐⭐) |
| Balsn CTF 2021 | trinity | 0/284 (⭐⭐⭐⭐) |
| Dragon CTF 2021 | Baby MAC | 89/247 (⭐⭐) |
| Dragon CTF 2021 | CRC Recursive Challenge (warmup) | 11/247 (⭐⭐⭐) |
| Dragon CTF 2021 | CRC Recursive Challenge 🔥 | 2/247 (⭐⭐⭐⭐) |
| HITCON CTF 2021 | a little easy rsa | 37/288 (⭐) |
| HITCON CTF 2021 | so easy rsa | 56/288 (⭐⭐) |
| HITCON CTF 2021 | magic rsa | 27/288 (⭐⭐) |
| HITCON CTF 2021 | magic dlog | 27/288 (⭐⭐) |
| HITCON CTF 2021 | so easy but not rsa | 15/288 (⭐⭐) |
| HITCON CTF 2021 | still not rsa | 12/288 (⭐⭐⭐) |
| SECCON CTF 2021 | pppp | 70/506 (⭐) |
| SECCON CTF 2021 | oOoOoO | 26/506 (⭐⭐) |
| SECCON CTF 2021 | CCC | 17/506 (⭐⭐) |
| SECCON CTF 2021 | cerberus | 16/506 (⭐⭐) |
| SECCON CTF 2021 | XXX | 14/506 (⭐⭐⭐) |
| SECCON CTF 2021 | Sign Wars | 8/506 (⭐⭐⭐) |
| hxp CTF 2021 | gipfel | 109/150 (⭐) |
| hxp CTF 2021 | kipferl | 35/150 (⭐⭐) |
| hxp CTF 2021 | zipfel 🔥 | 5/150 (⭐⭐⭐⭐) |
| hxp CTF 2021 | infinity | 11/150 (⭐⭐⭐⭐) |
| hxp CTF 2021 | f_cktoring 🔥 | 3/150 (⭐⭐⭐⭐) |
| hxp CTF 2021 | caBalS puking 🔥 | 6/150 (⭐⭐) |
| ASIS CTF Finals 2021 | Stairs | 43/198 (⭐) |
| ASIS CTF Finals 2021 | RAS | 36/198 (⭐) |
| ASIS CTF Finals 2021 | nDLP | 37/198 (⭐) |
| ASIS CTF Finals 2021 | mDLP | 30/198 (⭐) |
TSG CTF 2021⌗
Beginner's Crypto 2021⌗
- Solves: 126/775
- Difficulty: ⭐
- Tags:
rsa
We are given $p$ and $q$, the primes for RSA. Denote $n = pq$. We are also given the flag $c_1, c_2, c_3$ encrypted with the same modulus but different exponents. Those exponents, $e_1, e_2, e_3$, are computed by
\[\begin{aligned} & e_1 = e^{65537}\ \text{mod}\ \varphi(n) \\ & e_2 = (e + 2)^{65537}\ \text{mod}\ \varphi(n) \\ & e_3 = (e + 4)^{65537}\ \text{mod}\ \varphi(n) \end{aligned}\]
Note that $e$, $e+2$ and $e+4$ are all primes. The objective is to recover the flag.
Minimalist's Private⌗
- Solves: 49/775
- Difficulty: ⭐⭐
- Tags:
rsa
We are given a RSA public key $(n, e)$ and a ciphertext $c$. Additionally, $\lambda(n)$ (the order of $\mathbb{Z}^*_n$) satisfies
\[\lambda(n)^2 \leq 10000n.\]
The objective is to decrypt $c$ for the flag.
Baba is Flag⌗
- Solves: 34/775
- Difficulty: ⭐⭐
- Tags:
ecdsa
When connected to the server, a ECDSA private key $d$ for SECP256k1 is generated. We are allowed to perform the below operations in a total of five times:
- [Sign] We will be given a signature of
Baba. The ECDSA is slightly modified (will be described below) and the nonce $k$ is around 80 bits. - [Find rule] We will be asked to send a message $m$ and the signature $(r, s)$. It would return the flag if we have a valid signature for message
Flag.
For ECDSA, $s = k^{-1} (z + rd_A)\ \text{mod}\ n$. However in this challenge, $s$ is computed by
\[k^{-1} (z + d_A)\ \text{mod}\ n.\]
The objective is to forge a signature for the message Flag.
Flag is Win⌗
- Solves: 10/775
- Difficulty: ⭐⭐⭐
- Tags:
ecdsa
When connected to the server, a ECDSA private key $d$ for SECP256k1 is generated. We are allowed to perform the below operations in a total of five times:
- [Sign] We will be given a signature of
Baba. The nonce $k$ is around 80 bits. - [Find rule] We will be asked to send a message $m$ and the signature $(r, s)$. It would return the flag if we have a valid signature for message
Flag.
The objective is to forge a signature for the message Flag.
This is DSA⌗
- Solves: 9/775
- Difficulty: ⭐⭐
- Tags:
dsa
The challenge uses a modified pycryptodome package with the below code difference:
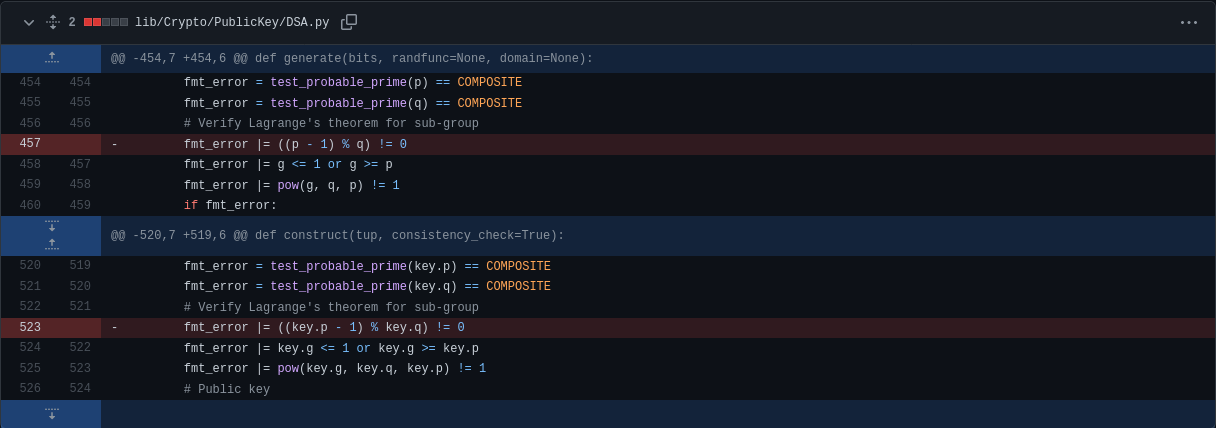
When connected to the server, we are given a 256-bit order $q$ and is asked a 2048-bit $p$ and $h$. The generator $g$ is computed by
\[g = h^{\lfloor{(p-1)/q\rfloor}}\ \text{mod}\ p.\]
Also, a private key $x \in [0, q)$ is generated and the public key $y$ is given by
\[y = g^x\ \text{mod}\ p.\]
We will be given $g$ and $y$. The goal is to craft a signature of flag in 15 seconds.
TastelessCTF 2021⌗
crybaby 🔥⌗
- Solves: 14/162
- Difficulty: ⭐⭐⭐
- Tags:
gcm
When connected to the server, a 16-byte AES key $\mathcal{K}$ is generated. There are two stages and during the $k$-th stage, we are given the $k$-th oracle $\mathcal{O}_k$. We are able to call the oracles as much as we could (unless an exception is thrown).
$\mathcal{O}_1$ uses AES-CTR and it asks for nonce $\mu$ and ciphertext $c$. It returns
\[\text{Encrypt}_\mathcal{K}(\mu, \text{Login successful!})\]
and proceed to the next stage if $\text{Decrypt}_\mathcal{K}(\mu, c)$ is equal to
adminplz, and otherwise\[\text{Encrypt}_\mathcal{K}(\mu, \text{Unknown command!}).\]
$\mathcal{O}_2$ uses AES-GCM and it asks for nonce $\mu$ and ciphertext $c$. It returns
\[\text{Encrypt}_\mathcal{K}(\mu, \mathcal{F})\]
if $\text{Decrypt}_\mathcal{K}(\mu, c)$ is equal to
flagplz, and otherwise\[\text{Encrypt}_\mathcal{K}(\mu, \text{Unknown command!}).\]
The objective is to recover the flag $\mathcal{F}$.
pbctf 2021⌗
Alkaloid Stream⌗
- Solves: 132/210
- Difficulty: ⭐⭐
- Tags:
math
Suppose that the flag is $m$ bits long ($m = 600$ in this challenge). Initially, an invertible $m\times m$ matrix in $\text{GF}(2)$ (denote by $\mathcal{K}$) is generated and is interpreted as $m$ $m$-bit integers, 0 <= key[0], key[1], ..., key[m-1] < 2^m. A keystream and a public key is generated from the key by the function gen_keystream, defined below:
def gen_keystream(key):
ln = len(key)
# Generate some fake values based on the given key...
fake = [0] * ln
for i in range(ln):
for j in range(ln // 3):
if i + j + 1 >= ln:
break
fake[i] ^= key[i + j + 1]
# Generate the keystream
res = []
for i in range(ln):
t = random.getrandbits(1)
if t:
res.append((t, [fake[i], key[i]]))
else:
res.append((t, [key[i], fake[i]]))
for r in res:
print(r)
# Shuffle!
random.shuffle(res)
keystream = [v[0] for v in res]
public = [v[1] for v in res]
return keystream, publicWe are given a public key and the flag xorred with the keystream. The objective is to recover the flag.
Steroid Stream⌗
- Solves: 38/210
- Difficulty: ⭐⭐
- Tags:
math
The challenge is similar to Alkaloid Stream, except that $m = 616$ and gen_keystream is defined below:
def gen_keystream(key):
ln = len(key)
+ assert ln > 50
# Generate some fake values based on the given key...
fake = [0] * ln
- for i in range(ln):
- for j in range(ln // 3):
- if i + j + 1 >= ln:
- break
- fake[i] ^= key[i + j + 1]
+ for i in range(ln - ln // 3):
+ arr = list(range(i + 1, ln))
+ random.shuffle(arr)
+ for j in arr[:ln // 3]:
+ fake[i] ^= key[j]
# Generate the keystream
res = []
for i in range(ln):
t = random.getrandbits(1)
if t:
res.append((t, [fake[i], key[i]]))
else:
res.append((t, [key[i], fake[i]]))
# Shuffle!
random.shuffle(res)
keystream = [v[0] for v in res]
public = [v[1] for v in res]
return keystream, publicGoodHash 🔥⌗
- Solves: 30/210
- Difficulty: ⭐⭐⭐
- Tags:
gcm
The digest for the hash algorithm GoodHash for the message $m$ is given by encrypting 32 null bytes with a known key goodhashGOODHASH with the nonce $m$. It is 48 bytes long, which composes of a 32-byte ciphertext and a 16-byte tag.
We are given a token {"token": "32 hex characters", "admin": false} when connected to the server, along with its corresponding hash $h_0$. The goal is to craft a JSON token token such that token['admin'] equals true, which also has the hash $h_0$.
Seed Me 🔥⌗
- Solves: 24/210
- Difficulty: ⭐⭐⭐
- Tags:
prng,lcg
We are asked a seed for the Java program. the random instance, rng, is defined by rng = new Random(seed). We will get the flag if the 2048-, 4096-, ..., 32768-th output from rng.NextFloat() are never less than $0.9801547$.
Yet Another PRNG 🔥⌗
- Solves: 14/210
- Difficulty: ⭐⭐⭐
- Tags:
prng
The outputs $r_0, r_1, r_2, ... \in [0, 2^{64})$ of the PRNG in the challenge is defined below:
\[r_k := 2m_1x_k - m_3y_k - m_2z_k\ \text{mod}\ M,\]
where $m_1, m_2, m_3$ are 32-bits and $M$ is a 64-bit known constants. Also, let $a_{ij}$ be 20-bit known constants and for $k \leq 3$,
\[ \begin{cases}\begin{aligned} x_k &:= a_{11} x_{k-3} + a_{12} x_{k-2} + a_{13} x_{k-1} \\ y_k &:= a_{21} y_{k-3} + a_{22} y_{k-2} + a_{23} y_{k-1} \\ z_k &:= a_{31} z_{k-3} + a_{32} z_{k-2} + a_{33} z_{k-1} \end{aligned}\end{cases}. \]
Note that we are not given $x_k, y_k, z_k$ for $k = 0, 1, 2$. Suppose that we have $r_0, r_1, ..., r_{11}$, and the flag is xor-ed with $r_{12}, r_{13}, ...$. The objective is to recover the flag.
Yet Another RSA 🔥⌗
- Solves: 12/210
- Difficulty: ⭐⭐⭐
- Tags:
rsa
We are given a RSA public key $n, e$ and an encrypted flag $c$. Hereby $n$ is 1024-bit number which is a product of two 512-bit primes $p, q$ (they are both in the form of $a^2 + 3b^2$). It is also known that $d$ is 400-bit long.
Remarkably, the multiply operation is performed under a group $\mathcal{G}$ with
\[\mathcal{G} = \mathbb{Z}_n^2 \cup (\mathbb{Z}_n\times\{\varepsilon\}) \cup \{\varepsilon\}^2.\]
Also $|\mathcal{G}| = (p^2+p+1)(q^2+q+1)$. The objective is to recover the flag from $c$.
# Note: The challenge used `add` but I think it would be better to call it `multiply`.
def multiply(P, Q, mod):
m, n = P
p, q = Q
if p is None:
return P
if m is None:
return Q
if n is None and q is None:
x = m * p % mod
y = m + p % mod
return (x, y)
if n is None and q is not None:
m, n, p, q = p, q, m, n
if q is None:
if (n + p) % mod != 0:
x = (m * p + 2) * inverse(n + p, mod) % mod
y = (m + n * p) * inverse(n + p, mod) % mod
return (x, y)
elif (m - n ** 2) % mod != 0:
x = (m * p + 2) * inverse(m - n ** 2, mod) % mod
return (x, None)
else:
return (None, None)
else:
if (m + p + n * q) % mod != 0:
x = (m * p + (n + q) * 2) * inverse(m + p + n * q, mod) % mod
y = (n * p + m * q + 2) * inverse(m + p + n * q, mod) % mod
return (x, y)
elif (n * p + m * q + 2) % mod != 0:
x = (m * p + (n + q) * 2) * inverse(n * p + m * q + r, mod) % mod
return (x, None)
else:
return (None, None)Hack.lu CTF 2021⌗
Silver Water Industries⌗
- Solves: 92/174
- Difficulty: ⭐⭐
- Tags:
math
When connected to the server, a modulus $n = pq$ is generated with $p, q$ be 64 bits, $p \equiv 1\ (\text{mod}\ 4)$ and $q \equiv 3\ (\text{mod}\ 4)$. To encrypt a bit $m$, a quadratic non-residue of $n$ (denoted by $x$) is generated. The ciphertext would be $x^2 (-1)^m\ \text{mod}\ n$.
A token of 20 bytes is encrypted and we have the encrypted token. The objective is to recover the token, which we could win the flag if we send them the correct one.
WhatTheHecc⌗
- Solves: 45/174
- Difficulty: ⭐⭐
- Tags:
ecc
The challenge defines a signature algorithm $\mathcal{S}$, where a key generated with elliptic curve parameter P-256 (the public and private keys are respectively $Q$ and $d$). The signing algorithm for a message $m$ is specified below ($\text{H}$ is the SHA3-256 algorithm that returns an integer given an array of bytes):
- Compute $r = \text{H}(m) \cdot Q$
- Compute $r' = r\cdot d^{-1}\ \text{mod}\ q$, where $q$ is the order of the curve
- Define $z = n_\text{nonce} | t$, where $n_\text{once} \in [1, q)$ and $t$ is the timestamp in seconds
- Compute $R = r' + \text{H}(z) \cdot G$
- Compute $s = [d - \text{H}(z)]\ \text{mod}\ q$
- Return $(R, s)$ as the signature.
Also the verifying algorithm for a message $m$ and signature $(R, s)$:
- If $s = 0\ \text{or}\ 1$ and $s > 0$ then the signature is considered invalid.
- The signature is valid only if
\[s \cdot G - Q + R = \text{H}(m) \cdot G\]
There are three functions those we can use when connected to the server:
- [Show] Prints the public key.
- [Sign] Signs one of the four commands:
id,uname,lsanddatewith $\mathcal{S}$. - [Run] Takes a signed command and executes if the signature is valid.
lwsr⌗
- Solves: 20/174
- Difficulty: ⭐⭐
- Tags:
lfsr,lwe
Suppose that $q = 16411$.
When connected to the server, a LWE private key $s \in \mathbb{Z}_q^{128}$ and 384 sets of public key $(p_1, r_1), (p_2, r_2), ..., (p_{384}, r_{384}) \in \mathbb{Z}_q^{128} \times \mathbb{Z}_q$ are also generated. Also, a LFSR state $t = (t_1, t_2, ..., t_{384})$ with $t_1, t_2, ..., t_{384} \in \{0, 1\}$ is generated.
The flag is encrypted bit-by-bit. The ciphertext of the $i$-th bit of the message, $m_i$, is defined by:
\[\begin{cases} c_{i, 0} &= (t_1 \cdot p_1 + t_2 \cdot p_2 + ... + t_{384} \cdot p_{384})\ \text{mod}\ q \\ c_{i, 1} &= (t_1 \cdot r_1 + t_2 \cdot r_2 + ... + t_{384} \cdot r_{384} + 8205m_i)\ \text{mod}\ q \end{cases}\]
Additionally, after a bit is encrypted, the LFSR state is updated with
\[(t'_1, t'_2, ..., t'_{384}) := \left(t_2, t_3, ..., \text{NEXT}(t_1, t_2, ..., t_{384})\right).\]
We are given $(p_1, r_1), (p_2, r_2), ..., (p_{384}, r_{384})$ and encrypted flag $(c_{1,0}, c_{1,1}), (c_{2,0}, c_{2,1}), ...$. We are then able to access the decryption oracle. The goal is to recover the flag.
BSides Ahmedabad CTF 2021⌗
dlppp⌗
- Solves: 39/314
- Difficulty: ⭐⭐
- Tags:
discrete log
Let $p$ be a 512-bit prime and $m$ be the flag. Let also $y = (1 + p)^m\ \text{mod}\ p^3$. We are given $p$ and $y$ and the objective is to recover the flag.
floorsa⌗
- Solves: 27/314
- Difficulty: ⭐⭐
- Tags:
rsa,math
Let $p$ and $q$ be 1024-bit prime and $n = p\cdot q$ be a 2048-bit RSA modulus. Let $e = 65537$ and $m$ be the secret message. We are given the $n$ and the ciphertext $c = m^e\ \text{mod}\ n$. Additionally, we are given
\[s = \sum_{k=0}^{q-1} \lfloor{\frac{p\cdot k}{q}}\rfloor.\]
The objective is to recover the secret message $m$.
SSSS.RNG 🔥⌗
- Solves: 16/314
- Difficulty: ⭐⭐
- Tags:
lcg
Let $p$ be a 512-bit prime and $a, b, g_0 \in [2, p)$. Let $\mathcal{G}$ be a PRNG and let $g_k$ be the $k$-th output from $\mathcal{G}$, given by
\[g_k = (a\cdot g_{k-1} + b)\ \text{mod}\ p.\]
Let $\text{f}(x) := g_1 + g_2 x + g_3 x^2 + g_4 x^3 + g_5 x^4 + g_6 x^5$ be a polynomial over $\mathbb{Z}_p$. Suppose that we are given $p$, $\text{f}(1), \text{f}(2), \text{f}(3), \text{f}(4)$ and $\text{f}(\text{flag})$. The objective is to compute $\text{flag}$.
ECC-RSA 2 🔥⌗
- Solves: 8/314
- Difficulty: ⭐⭐⭐
- Tags:
ecc,rsa
Let $n = p\cdot q$ with $p$ and $q$ being 512-bit primes. An elliptic curve $\mathcal{C}$ is given by:
\[\mathcal{C}:\quad y^2 \equiv x^3 + a x + b\ (\text{mod}\ n),\]
where $a = -3$. Let $P \in \mathcal{C}$ and let $m_0, m_1, ... \in [0, 256)$ be the characters of the flag. The $k$-th character of the flag $m_k$ is encrypted to $c_k$:
\[c_k \equiv ((2^k\cdot P)_x \cdot m_k)^{65537} \ (\text{mod}\ n).\]
Given $n, a, b$ and $c_0, c_1, ...$. It is known that the flag satisfies the format Neko{\w+}, the objective is to recover the flag.
They Were Eleven 🔥⌗
- Solves: 3/314
- Difficulty: ⭐⭐⭐⭐
- Tags:
rsa
Suppose that we have a 111-byte message $m$. Let $p_1, p_2, ..., p_{11}, q_1, q_2, ..., q_{11}$ be 512-bit primes and $r_1, r_2, ..., r_{11} \in [0, 2^{11})$.
We are given $n_i = p_i\cdot q_i$ and $c_i = m^{11}\cdot r_i\ \text{mod}\ n_i$ for $i = 1, 2, ..., 11$. The objective is to recover $m$.
HKCERT CTF 2021⌗
小諧星 / A Joke Cipher⌗
- Solves: 88/239
- Difficulty: ⭐
- Tags:
math
The challenge implements Nagaty's Cryptosystem1 which no one knows why it is a cryptosystem. Initially, a prime $p$ is determined. Alice and Bob respectively derive a private key $x_A$ and a public key $y_A := x_A\ \text{mod}\ p$ (resp. $x_B$ and $y_B := x_B\ \text{mod}\ p$). A shared key is computed by Alice with $s = y_A \cdot {y_B}^2 \cdot x_A\ \text{mod}\ p$. Finally, the message $m$ is encrypted by $m \cdot s$.
In the challenge, we are given $p$, $y_A$, $y_B$ and an encrypted flag $c$. The objective is to recover the flag.
Freedom / Cipher Mode Picker⌗
- Solves: 21/239
- Difficulty: ⭐
- Tags:
mode of operations
A 16-byte key and a 16-byte IV is generated when connected to the server. We are able to use each of the below encryption functions once, to encrypt either a given message or the 80-byte flag:
# 1. AES-ECB
cipher = AES.new(key, AES.MODE_ECB)
# 2. AES-CBC
cipher = AES.new(key, AES.MODE_CBC, iv)
# 3. AES-CFB
cipher = AES.new(key, AES.MODE_CFB, iv, segment_size=128)
# 4. AES-OFB
cipher = AES.new(key, AES.MODE_OFB, iv)
# 5. AES-CTR
cipher = AES.new(key, AES.MODE_CTR, counter=Counter.new(16, prefix=iv[:14]))The goal is to recover the flag.
長話短說 / Key Backup Service 1⌗
- Solves: 6/239
- Difficulty: ⭐⭐
- Tags:
rsa
When connected to the server, a 32-byte master secret $x$ is generated. We are able to call the below functions at a total of 17 times:
- [SEND] Returns the ciphertext, i.e., $m^e\ \text{mod}\ n$, of an arbitrary given message $m$ with the current key $\mathcal{K}$.
- [PKEY] Generates a set of RSA key and assign to $\mathcal{K} = (n, e)$.
- [BACKUP] Returns the encrypted secret, i.e., $x^{e}\ \text{mod}\ n$, with the current key $\mathcal{K}$.
- [FLAG] Encrypts the flag with the key $x$ under AES-CBC.
Additionally, the public exponent is $e = 17$ and the 512-bit primes for the moduli is generated by a PRNG, seeded by the below snippet:
# 256 bits for random-number generator
N = 0xcdc21452d0d82fbce447a874969ebb70bcc41a2199fbe74a2958d0d280000001
G = 0x5191654c7d85905266b0a88aea88f94172292944674b97630853f919eeb1a070
H = 0x7468657365206e756d6265727320617265206f6620636f757273652073757321
# The primes for the public exponent. id is a randomly generated 256-bit integer.
p = generate_prime(x + int.to_bytes(pow(G, id, N), 32, 'big'))
q = generate_prime(x + int.to_bytes(pow(H, id, N), 32, 'big'))Braceless / Key Backup Service 2⌗
- Solves: 5/239
- Difficulty: ⭐⭐
- Tags:
rsa
The challenge is identical to 長話短說 / Key Backup Service I, with three changes:
- $e = 17$ is changed to $e = 65537$,
- The number of oracle calls is increased from 17 to 65537,
- We do not have the netcat service anymore. Instead, we have a transcript of an interaction. It includes one
FLAGoperation, followed by 16384 sequences of the below operations:PKEY,SEND 2,SEND 3andBACKUP.
FreeRider / Tenet: The Plagarism⌗
- Solves: 4/239
- Difficulty: ⭐⭐
- Tags:
ctr
Suppose that the flag matches the regular expression hkcert21\{\w{35}\}. We define an encryption algorithm, $\mathcal{E}$, with a 16-byte key $k_1k_2...k_{16}$. Let $m$ be the message we would like to encrypt (all of the counters are set to zero):
- Encrypt $m$ with AES-CTR using the key
k1 00 00 00 ... 00($k_1$ followed by 15 null bytes) and denote it by $t_1$. - Encrypt $t_1$ with AES-CTR using the key
k2 00 00 00 ... 00and denote it by $t_2$. - ...
- Encrypt $t_{15}$ with AES-CTR using the key
k16 00 00 00 ... 00and denote it by $t_{16}$. - Return $t_{16}$ as the ciphertext.
$\mathcal{E}$ is used to encrypt the message Congratulations! [FLAG] and we are given its ciphertext. The objective is to recover the flag. Notably, the challenge is highly referenced from Tenet in HKCERT CTF 2020.
集合吧!地球保衛隊 / Sratslla SEA⌗
- Solves: 2/239
- Difficulty: ⭐⭐⭐
- Tags:
aes
We will use the Advanced Encryption Standard (AES) for encryption in the challenge. Let $k_0k_1k_2...k_{15}$ be a 16-byte key and let $K_n := k_nk_nk_nk_n$ for $n = 0, 1, 2, ..., 15$. When connected to the server, $k_0k_1k_2...k_{15}$ is randomly created and we are able to access the below functions for 128 times:
- [ark secret] encrypts $K_0K_1K_2K_3$ without the
AddRoundKeyoperation and returns the ciphertext. - [sb secret] encrypts $K_4K_5K_6K_7$ without the
SubBytesoperation and returns the ciphertext. - [sr secret] encrypts $K_8K_9K_{10}K_{11}$ without the
ShiftRowsoperation and returns the ciphertext. - [mc secret] encrypts $K_{12}K_{13}K_{14}K_{15}$ without the
MixColumnsoperation and returns the ciphertext. - [ark data] (resp. [sb data], [sr data] or [mc data]) encrypts a 16-byte user-defined data without the
AddRoundKeyoperation (resp.SubBytes,ShiftRowsorMixColumns) and returns the ciphertext.
We are also given a 64-byte encrypted flag when connected to the server. The goal is to collect enough information for the key in 128 calls and decrypt for the flag.
約定的夢幻島 / Sign In Please, Again⌗
- Solves: 2/239
- Difficulty: ⭐⭐⭐
- Tags:
hash
Define the below authentication algorithm $\mathcal{P}$. Suppose that a user have a $n$ character-long password, $p_1p_2...p_n$:
- The server generates a 4-byte salt $s_1s_2s_3s_4$ and generate a permutation of $\{1, 2, ..., n+5\}$, denote it as $\sigma$.
- A user
- generates one byte of pepper $r$,
- denotes $x_k = p_k$ for $k = 1, 2, ..., n$, $x_{n+k} = s_k$ for $k = 1, 2, ..., 4$ and $x_{n+5} = r$,
- computes $y_k = x_{\sigma(k)}$ for $k = 1, 2, ..., n+5$ and $h := \text{SHA256}(y_1y_2...y_{n+5})$, and
- send $h$ to the server.
- The server computes $h'$ from $p_1p_2...p_n$, the salt $s_1s_2s_3s_4$ and all $r \in [0, 256)$. If there exists $r$ such that $h = h'$, the user is authenticated.
The netcat service implements the above algorithm $\mathcal{P}$ and the player, who acts as the man in-the-middle, can play with below operations in a total of 50 times:
- [🕵️] The player impersonates the server and sends a salt $s_1s_2s_3s_4$ and surjective mapping $\sigma: \{1, 2, ..., k\} \rightarrow \{1, 2, ..., 21\}$ to the user. The user replies with a digest $h$. By surjective $\sigma$ should satisfy the below condition:
- For all $v = 1, 2, ..., 21$, there exists $u \in \{1, 2, ..., k\}$ such that $\sigma(u) = v$.
- [🖥️] The server sends a permutation $\sigma$ and a salt $s_1s_2s_3s_4$. If the player supplies with a valid digest $h$, the server replies with the flag.
Balsn CTF 2021⌗
1337 pins⌗
- Solves: 5/284
- Difficulty: ⭐⭐⭐
- Tags:
mt19937
When connected to the server, we are asked to guess $r_1, r_2, ..., r_{31337}$, the consecutive outputs from random.getrandbits(32) % 10. On the $k$-th turn we are asked to guess $r_k$. If the guess is incorrect, $r_k$ will be printed. The objective is to predict and submit 1337 consecutive outputs.
dlog 🔥⌗
- Solves: 2/284
- Difficulty: ⭐⭐⭐⭐
- Tags:
discrete log,timing attack
Suppose that $p = 2q+1$ where $p, q$ are primes. Let also $s$ be an exponent. We are given that $0 < p < 2^{1025}$ and $0 < s < 2^{100}$. Given three APIs:
/oraclereceives $x$ and returns $x^s\ \text{mod}\ p$,/flagreceives $x$. If $x^s\ \text{mod}\ p = 1337$ the flag will be returned,/metricsreturns metrics including the total number of calls and the total time on processing/oracleand/flag.
The objective is to retrieve the flag.
trinity⌗
- Solves: 0/284
- Difficulty: ⭐⭐⭐⭐
- Tags:
hash
Given a hash key $k$ for $\text{Blake}_3$, the Blake-3 algorithm returning 64 bits as a digest. The objective is to find three distinct messages $m_1, m_2, m_3$ such that
\[\text{Blake}_3(m_1, k) = \text{Blake}_3(m_2, k) = \text{Blake}_3(m_3, k).\]
Dragon CTF 2021⌗
Baby MAC⌗
- Solves: 89/247
- Difficulty: ⭐⭐
- Tags:
block cipher
When connected to the server, a 16-byte key $\mathcal{K}$ is generated. Define the signature algorithm $\mathcal{S}$ of message $m$:
- Set $s \leftarrow 0$ (16 null bytes).
- Pad $m$ with PKCS7 and break it down into blocks of 16 bytes: $m_1, m_2, ..., m_n$.
- For $i = 1, 2, ..., n$, update $s \leftarrow \text{Enc}_\mathcal{K}(s \oplus m_i)$.
- Update $s \leftarrow \text{Enc}_\mathcal{K}(s)$.
- Return $s$.
We are given an oracle to compute $\mathcal{S}(m)$ whenever $m$ does not contain gimme flag. The objective is to craft a signature of a message that contains gimme flag.
CRC Recursive Challenge (warmup)⌗
- Solves: 11/247
- Difficulty: ⭐⭐⭐
- Tags:
crc
The objective is to find a message which correctly depicts its CRC-64 digest.
def crc64(buf, crc=0xffffffffffffffff):
for val in buf:
crc ^= val << 56
for _ in range(8):
crc <<= 1
if crc & 2**64:
crc ^= 0x1ad93d23594c935a9
return crc
inp = input().strip().encode()
crc = crc64(inp)
if inp == f'My crc64 is 0x{crc:016x}! Cool, isn\'t it?'.encode():
with open('flag.txt', 'r') as f:
print(f.read().strip())
else:
print('Nope!')CRC Recursive Challenge 🔥⌗
- Solves: 2/247
- Difficulty: ⭐⭐⭐⭐
- Tags:
crc
The objective is to find a message which correctly depicts its CRC-128 digest.
def crc128(buf, crc=0xffffffffffffffffffffffffffffffff):
for val in buf:
crc ^= val << 120
for _ in range(8):
crc <<= 1
if crc & 2**128:
crc ^= 0x14caa61b0d7fe5fa54189d46709eaba2d
return crc
inp = input().strip().encode()
crc = crc128(inp)
if inp == f'My crc128 is 0x{crc:032x}! Cool, isn\'t it?'.encode():
with open('flag.txt', 'r') as f:
print(f.read().strip())
else:
print('Nope!')HITCON CTF 2021⌗
a little easy rsa⌗
- Solves: 37/288
- Difficulty: ⭐
- Tags:
rsa
Let $p$ and $q$ are primes of respectively 211 and 815 bits. Let $d = p$ and $n = pq$ be the private key and the public modulus of RSA. We are given $e = d^{-1}\ \text{mod}\ \phi(n)$, $n$ and the encrypted flag $c$. The objective is to recover the flag.
so easy rsa⌗
- Solves: 56/288
- Difficulty: ⭐⭐
- Tags:
lcg,rsa
We are given the parameters of the LCG that is used to generate primes for RSA, namely, $r_A$, $r_B$ and $r_M$ (all of them are 512-bit primes). Let $x_0$ be the seed and the $k$-th output is defined by
\[x_k = (r_Ax_{k-1} + r_B)\ \text{mod}\ r_M.\]
Suppose that $p = x_m$ and $q = x_{m+\Delta m}$ ($x_{m+1}, x_{m+2}, ..., x_{m+\Delta m-1}$ are not primes). We are also given $n = pq$, $e = 65537$ and the encrypted flag $c$. The objective is to recover the flag.
magic rsa⌗
- Solves: 27/288
- Difficulty: ⭐⭐
- Tags:
dlog
We are given 136-bit $n_0$ and is asked to construct a 384-bit $n$ such that the first 136-bit of $n$ is $n_0$. The objective is to find $m$ and $e$ such that:
- $h = m^e\ \text{mod}\ n$, and
- $h = \text{SHA384}(m)$.
magic dlog⌗
- Solves: 27/288
- Difficulty: ⭐⭐
- Tags:
dlog
The challenge is similar to magic rsa, except that $n$ this time needs to be a prime.
so easy but not rsa⌗
- Solves: 15/288
- Difficulty: ⭐⭐
- Tags:
ntru,prng
We are given a transcript that contains
- an encrypted flag,
- a NTRU public key,
- 200 pairs of 240-bit random message and its corresponding ciphertext.
Notably the Python's random (i.e. MT19937) is used to generated the random messages and the polynomials those are used as a random source for encryption. The objective is to recover the encrypted flag.
still not rsa⌗
- Solves: 12/288
- Difficulty: ⭐⭐⭐
- Tags:
ntru
When connected to the server, a polynomial $p_\text{priv}$ with below properties is generated.
- $p_\text{priv}$ is of degree $\leq 167$,
- $p_\text{priv}$ has 61 terms with coefficient being 1,
- $p_\text{priv}$ has 60 terms with coefficient being -1, and
- There exists $q_{128} \in \mathbb{Z}_{128}[x]/(x^{167} - 1)$ and $q_{3} \in \mathbb{Z}_3[x]/(x^{167} - 1)$, such that
\[p_\text{priv} \cdot q_{128} = 1 \quad\land\quad p_\text{priv} \cdot q_3 = 1.\]
We are given $p_\text{pub} \in \mathbb{Z}_{128}[x]/(x^{167} - 1)$ where $p_\text{pub} \cdot p_\text{priv} = 3 \cdot r$, where $r$ has a low Hamming weight. We are also allowed to access the decryption oracle $\mathcal{D}$ 1000 times, which takes the ciphertext $c \in \mathbb{Z}_{128}[x]/(x^{167}-1)$ and perform:
- Compute $a = c \cdot p_\text{priv} \in \mathbb{Z}_{128}[x]/(x^{167}-1)$.
- Compute $m = a \cdot q_3 \in \mathbb{Z}_{3}[x]/(x^{167}-1)$.
- Return $m$ as the plaintext.
Additionally, when performing steps 1 and 2 of decryption, the coefficients are taken such that they have the smallest magnitude. For example,
- $63 x^2 + 64 x + 65$ will be reduced to $63 x^2 - 64 x - 63$ under modulo 128, while
- $2x^5 + 3x^4 + 4x^3 + 5x^2 + 6x + 7$ will be reduced to $x^5 + x^3 - x^2 + 1$ under modulo 3.
The objective is to recover $p_\text{priv}$.
SECCON CTF 2021⌗
pppp⌗
- Solves: 70/506
- Difficulty: ⭐
- Tags:
rsa,math
Let $n = pq, e = 65537$ be a RSA public key ($p$ and $q$ are 512-bit long). The flag is broken into two parts $m_1, m_2$ such that $m_1, m_2 < 2^{256}$. Let $M$ be the matrix
\[\left[\begin{matrix} r_1p & r_2p & r_3p & r_4p \\ 0 & r_5m_1 & r_6m_1 & r_7m_1 \\ 0 & 0 & r_8m_2 & r_9m_2 \\ 0 & 0 & 0 & r_10 \end{matrix}\right].\]
Here $r_1, r_2, ..., r_{10}$ are 768-bit primes. We are given $n, e$ and $M^e\ \text{mod}\ n$. The objective is to recover $(m_1, m_2)$ for the flag.
Credits: grhkm.
oOoOoO⌗
- Solves: 26/506
- Difficulty: ⭐⭐
- Tags:
knapsack
A message that matches the regular expression /^[oO]{128}$/ is generated. We are given a 640-bit prime $m$ and $s := \text{message}\ \text{mod}\ m$. The objective is to recover the message in 600 seconds.
CCC⌗
- Solves: 17/506
- Difficulty: ⭐⭐
- Tags:
rsa
We are given a RSA public key $(n, e = 65537)$ and an encrypted flag $c$. Suppose that the primes of $n$ is generated by:
- $p$ is 1024-bit prime,
- $q = \hat{p} + 3\hat{p} \cdot b + b^2$ is a prime ($\hat{p} = 23p$ and $b$ is a 691-bit integer).
The objective is to recover the flag.
cerberus⌗
- Solves: 16/506
- Difficulty: ⭐⭐
- Tags:
pcbc
When connected to the server, an encrypted flag in AES-PCBC $(\hat{\nu}, \hat{c})$ is given ($\hat{\nu}$ is the IV and $\hat{c}$ is the ciphertext). We are given a padding oracle that takes $(\nu, c)$, where $c$ starts with $\hat{c}$, and returns whether the PKCSv5 padding for the decrypted message is valid. The objective is to recover the flag.
XXX⌗
- Solves: 14/506
- Difficulty: ⭐⭐⭐
- Tags:
ecc
Suppose that the flag $x_0$ is 40 bytes long. We are given a 796-bit prime $p$ and six elliptic curves $C_1, C_2, ..., C_6$ over $\mathbb{Z}_p$ such that $(x_0, y_k) \in C_k$, where $y_k \in [2, x_0]$ is a random integer. The objective is to recover the flag $x_0$.
Sign Wars⌗
- Solves: 8/506
- Difficulty: ⭐⭐⭐
- Tags:
ecdsa,prng
The challenge is defined over the elliptic curve P-384. There are two stages:
sign_prequeluses the first 48 bytes of the flag as the secret key. A 16-byte message $z_1$ is signed 80 times and we are given their signatures $(r, s)$. Note that the supposingly secure random $k$ in ECDSA is defined by $k = k_1 + 2^{128} z_1 + 2^{256} k_3$, where $k_1, k_3$ are generated byrandom.getrandbits(128).sign_originaluses the first 48 bytes of the flag as the secret key. A 16-byte message $z_2$ is signed 3 times and we are given their signatures $(r, s)$. Note that $k$ this time is generated byrandom.getrandbits(384).
Note that we are not given the messages $z_1, z_2$.
hxp CTF 2021⌗
gipfel⌗
- Solves: 109/150
- Difficulty: ⭐
- Tags:
dh
We are given a prime $q$ such that $q = 4p^2 + 1$ for some prime $p$. When connected to the server, an integer password $\text{pw} \in \mathbb{Z}_{10^6}$ is generated. We are allowed to attempt handshake three times.
In each handshake attempt, $g = \mathcal{H}(p)$ is derived ($\mathcal{H}$ is a known deterministic hash function) and the server's secret key $x_A \in 40 \cdot \mathbb{Z}_{2^{999}}$ is generated.
- We are given the server's public key $y_A := \mathcal{F}(g, x_A)$.
- We are asked to give $y_B \in [2, q)$.
- The server computes $s := \mathcal{F}(y_B, x_A)$.
- We are given $\text{ver}_A := \mathcal{F}(g, s^3)$.
- We are asked to give $\text{ver}_B$.
- If $\text{ver}_B = \mathcal{F}(g, s^5)$, then we are given the flag encrypted with AES-CTR where the key is derived by $\text{pw}$ and $s$. Otherwise, we will be given $s$.
Finally, here $\mathcal{F}$ is given by $\mathcal{F}(a, n) = a^n\ \text{mod}\ q$. The goal is to recover the flag.
kipferl⌗
- Solves: 35/150
- Difficulty: ⭐⭐
- Tags:
ecdh
The challenge is similar to gipfel except that $\mathcal{F}$ is given by $\mathcal{F}(a, n) = (n \cdot G)_x$, with $a$ being the x-coordinate of $G$ on the curve $\mathcal{C}: y^2 = x^3 + x$. Note that $\mathcal{F}$ did not check if there exists a $P \in \mathcal{C}$ such that its x-coordinate equals $a$.
zipfel 🔥⌗
- Solves: 5/150
- Difficulty: ⭐⭐⭐⭐
- Tags:
ecdh
The challenge is similar to zipfel except that we are no longer given $\text{ver}_A$.
infinity⌗
- Solves: 11/150
- Difficulty: ⭐⭐⭐⭐
- Tags:
csidh
When connected to the server, it generates a CSIDH ($n = 29$, $p = 4 l_1 l_2 ... l_n - 1$ where $l_k$ is the $k$-th prime, $C = 2$) private key. We are asked to perform key exchange 500 times and we are given the shared key.
The goal is to recover the server's private key (which is used to derive an encryption key to encrypt the flag).
f_cktoring 🔥⌗
- Solves: 3/150
- Difficulty: ⭐⭐⭐⭐
- Tags:
rsa
We are given a RSA modulus $n$ and an encrypted flag $c$, where $n$ is a product of zero primes generated by gen_prime given below. The objective is to recover the flag.
R = __import__('random').SystemRandom().randint
def gen_prime():
while True:
p = (ZZ^2).0
while p.norm() < 5^55:
a,b = ((-1)^R(0,1)*R(1,7^y) for y in (2,1))
p *= matrix([[a,b],[123*b,-a]])
p += (ZZ^2).0
p *= diagonal_matrix((1,123)) * p
if is_pseudoprime(p):
return pcaBalS puking 🔥⌗
- Solves: 6/150
- Difficulty: ⭐⭐
- Tags:
application,signal
We are given two Signal backup files, one of which represents the state of an empty account. The objective is to recover the flag from the backup files.
ASIS CTF Finals 2021⌗
Stairs⌗
- Solves: 43/198
- Difficulty: ⭐
- Tags:
math
An asymmetric cipher is defined in this challenge. A composite $n$ is used as the public key and the ciphertext of a message $m$ is given by
\[\text{Enc}(m) = (m^5 + m)\ \text{mod}\ n.\]
When connected to the server, a public key is generated and given. We are also given the encryption oracle - for any given message $m$ we will retrieve $\text{Enc}(m + f)$ where $f$ is the flag. The objective is to recover the flag.
RAS⌗
- Solves: 36/198
- Difficulty: ⭐
- Tags:
rsa
We are given a RSA public key $(n = pq, e)$ and the encrypted flag $c$. Here $p$ and $q$ are generated so that there are $2 \leq a_p, a_q < 512$, $32 \leq b_p, b_q < 512$ and $0 \leq d_p, d_q < 2^{31}$ with
\[p = {a_p}^{b_p} + {d_p}\qquad\text{and}\qquad q = {a_q}^{b_q} + {d_q}.\]
The objective is to recover the flag.
nDLP⌗
- Solves: 37/198
- Difficulty: ⭐
- Tags:
discrete log
We are given $g, n, y \in \mathbb{Z}$ (as below) such that $g^x \equiv y\ (\text{mod}\ n)$ for a secret $x$. The objective is to recover $x$ (the flag).
g = 685780528648223163108441
n = 12588567055208488159342105634949357220607702491616160304212767442540158416811459761519218454720193189
y = 9136134187598897896238293762558529068838567704462064643828064439262538588237880419716728404254970025mDLP⌗
- Solves: 30/198
- Difficulty: ⭐
- Tags:
discrete log
An asymmetric cipher is defined in this challenge. Let $p$ be a prime and $d \in [2, p)$ be the private key. The public key is given by $(A, Q) \in \text{GL}_2(p) \times \text{GL}_2(p)$ with $Q = A^d$. A ciphertext $(C, E) \in \text{GL}_2(p) \times \text{GL}_2(p)$ of the message $M \in \text{GL}_2(p)$ is given by:
\[\begin{cases} C = A^r \\ E = Q^r \cdot M \end{cases},\]
where $r \in [2, p)$ is randomly generated. We are given a prime $p$ and the four matrices $A, Q, C, E \in \text{GL}_2(p)$ (as below). The objective is to recover $M$, i.e., the flag.
p = 94413310751917369305079812653655619566021075449954923397392050181976939189891
A = [
[38199337272663519912859864066101528484023656231849338967558894235177040565160, 39708167173513090810083500967474691943646789486489990958101592717502452906918],
[ 8216211510625558273096642057121313417997488994504871245106775381995665925783, 56213973479253849392219948587554091081997419218105584429833155946799898624740]
]
Q = [
[61709241598677561125021718690991651934557899286972116933820920757636771220273, 1945367449329759288724720626216309893787847192907494307536759223359193510642],
[37495232301500074672571996664644922614693962264764098174213150757616575323566, 7348269231944161963123250652171976847627786311806728904368575861561449853500]
]
C = [
[47566868540912475779105819546118874217903268597017385039977593878486632022506, 86073162301954995219912739344010659248720823814557810528618517154406350653517],
[23443866424088482893369441934221448179896589659663581973508963775891809430857, 74567333640177484678138574534395714128854315440076840728428649074147859070975]
]
E = [
[56937964695156855099385034285428853461603799261684034842341841781057485084327, 82459328835322885824854425864023809222717401981993182346342472865578156162544],
[85092677346274708324092648597361729755305119435989183201786866456596369562681, 22228861714953585357281182780002271505668586948202416054453861940155538803489]
]- Khaled A. Nagaty (2019) "A public key cryptosystem and signature scheme based on numerical series"
https://link.springer.com/content/pdf/10.1007/s42452-019-1928-8.pdf ↩