Dragon CTF 2020 is definitely had my best CTF moments. There are big brain moments and I have been mind-blown for multiple times during the game. This time we have teamed up with @blackb6a. I have solved all the crypto challenges and two challenges with my teammates.

There are three challenges writeup in this post:

  • Bit Flip (parts 2 and 3)
  • Frying in motion

Bit Flip (Crypto, 155+324+343 points)⌗

Challenge Summary⌗

At the beginning, a 128-bit alice_secret (denoted as $a$) is generated. We are given an oracle that allows us to input a 256-bit value $v$. An PRNG $R$ uses $a\oplus v$ to derive:

  1. a 512-bit prime $p$ that is used for Diffie-Hellman, and
  2. a 64-bit secret $a$ that is Alice's secret key.

For each oracle call, the following will be printed

  1. The number of rng.getbits(512) calls for $p$ to be a prime,
  2. Bob's public key (which is generated randomly in each call), $B$,
  3. The encrypted flag (with AES-CBC & key is derived from the DH shared key):

Of course, the devil is in the detail. The AES-CBC key is derived as follows:

dh_shared_key = 1337 ^ pow(B, a, p)
key = long_to_bytes(dh_shared_key, 16)[:16]

Furthermore, the PRNG is simple. It is maintaining a 256-bit state $s$. 512-bit and 64-bit numbers are generated respectively with:

def getbits(bits=512):
    output = sha256(long_to_bytes(s, 32)).digest() + sha256(long_to_bytes(s+1, 32)).digest()
    s += 2
    return output

def getbits(bits=64):
    output = sha256(long_to_bytes(s, 32)).digest()[-8:]
    s += 1
    return output

The plot twist⌗

This is the setting for part one. Parts two and three are pretty similar though.

  • Parts 2 and 3 are not returning Bob's public key, and
  • Part 3 uses the prime $p$ and check if $q := 2p+1$ is a prime. The prime $q$ (instead of $p$) is used for DH.

Solution⌗

Part I: The real bit-flipping⌗

Bit Flip 1 was solved in about 45 minutes. Basically we are able to recover $v$ from the number of rng.getbits(512) calls. Since I am sure that there will be writeups on this part available online, I am skipping this part.

I am just going to admit that I am lazy.

Part II: A nightmare on long_to_bytes⌗

Bit Flip 3 was solved in 1 hour - and we were the first to solve. But wait, why isn't part II on Bit Flip 2? The reason is simply because just I cannot solve it (yet).

defund had the same question, too.

The prime used for Diffie-Hellman can be 513-bit long. This makes the AES key derivation interesting - as long_to_bytes(x, 16) actually prepend null bytes until the output size is a multiple of 16. For example:

>>> long_to_bytes(2**127, 16).hex()
'80000000000000000000000000000000'
>>> long_to_bytes(2**128, 16).hex()
'0000000000000000000000000000000100000000000000000000000000000000'

Luckily (or unluckily) the shared key can be as large as 513 bits long. In that case, the first block would be 00 00 ... 00 00 01 - and this is the AES key.

We do not even need to know Alice's nor Bob's key. Basically there is around 25% chance for the DH shared key to be 513-bit. When it happens, the constant key is used and we are able to decrypt the flag - DrgnS{C0nst_A3S_K3y_1111111111111!}. First blood 🩸!

Part III: Playing mind-games on Bit Flip 2⌗

Bit Flip 2 was solved in about 12 hours. I was mind-blown when I know da wae. Since the DH key could never be 513 bits long anymore, we can no longer exploit in the way as described in Bit Flip 3.

Wait. This made me very puzzled: How do we find the shared key (or $g^{ab}\ (\text{mod}\ p)$) if Bob is not telling us anything?

Basically we have three options:

  1. Make $a = 0$. This implies that $g^{ab} \equiv 1$, resulting in a constant key.
  2. Find $a$ and $p$ such that $g^a\in\mathbb{Z}_p^*$ has a small order. Hence $\{g^{ab}\in\mathbb{Z}_p^*\ |\ b\in\mathbb{Z}\}$ can be exhausted feasibly.
  3. Make $p$ 385-bit long (or 1-bit, 129-bit or 257-bit). Then we are able to reuse the exploit on Bit Flip 3.

There is a point of time that over 10 teams have solved Bit Flip 2 while only hxp and us have solved Bit Flip 3. If option 3 is the way to go, the number of solves would not be the same. Moreover, option 2 is barely possible in a perspective of math. That said, unless there is a vulnerability that I am not awared of, we may need to make $a = 0$. That is equivalent to rng.getbits(64) == 0 and thus a 64-bit proof-of-work. Possible?

During the research, I was wondering if there is a proof-of-work database that has a list of payloads with many trailing zeros as its hash. I was even wondering if there is someone ever able to solve a 64-bit proof-of-work (particularly on SHA256). Turns out I am too naive - some are able to solve a 76-bit proof-of-work in around 10 minutes. Who? The bitcoin network.

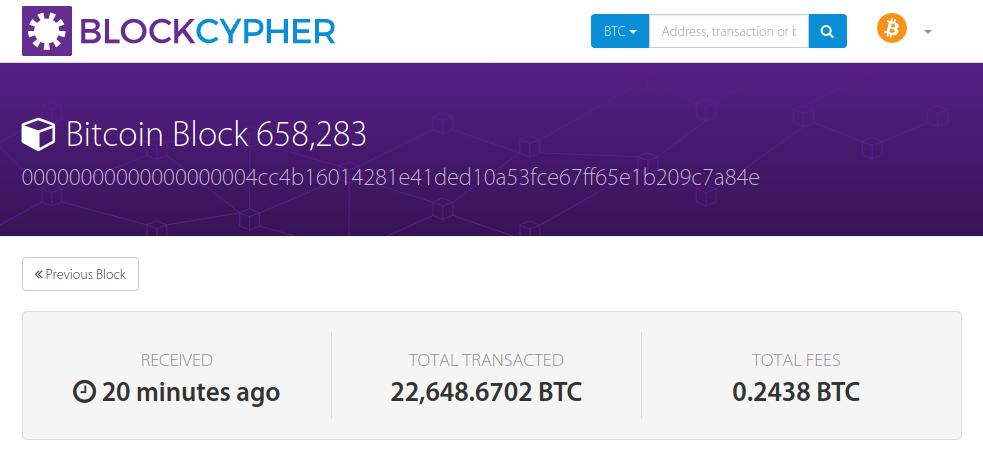
Let's appreciate the number of zeros...

The block hashing algorithm for Bitcoin is SHA256. This is how block 125552 (the smallest hash as of June 2011) is computed:

d = bytes.fromhex('0100000081cd02ab7e569e8bcd9317e2fe99f2de44d49ab2b8851ba4a30' +
                  '8000000000000e320b6c2fffc8d750423db8b1eb942ae710e951ed797f7' +
                  'affc8892b0f1fc122bc7f5d74df2b9441a42a14695')
m = hashlib.sha256(d).digest()
print(m.hex())
# b9d751533593ac10cdfb7b8e03cad8babc67d8eaeac0a3699b82857dacac9390
h = hashlib.sha256(m).digest()
print(h.hex())
# 1dbd981fe6985776b644b173a4d0385ddc1aa2a829688d1e0000000000000000

The above hash ends with 8 null bytes. If the below seed generates a prime in its first call of rng.getbits(512), then a = 0:

seed = 0xb9d751533593ac10cdfb7b8e03cad8babc67d8eaeac0a3699b82857dacac938c.

Unfortunately it is not. Luckily there are many inputs (available on the Bitcoin network) that generates eight trailing null bytes as its hash. We can simply look at the blocks and find the one we need. For me, I was using the block API from blockcypher.com to retrieve and compute the preimage of hashes. Eventually block 657972 satisfies our needs and the Alice's secret key will be $a = 0$.

That said, the AES key would be 00 00 ... 00 05 38 when $a = 0$ - and we are able to decrypt the flag: DrgnS{B1tc0in_p0w3r_crypt0_brut3}! 🎉

Frying in motion (Crypto, 324 points)⌗

Challenge Summary⌗

The challenge is simple. Upon connecting to the challenge server,

  • 257 HEX characters are generated, strfry-ed for 0x140000 times. Nothing is returned. (This took around 5 seconds)
  • Players are allowed to send up to 4096 bytes. The server returns the strfry-ed input.
  • 64 HEX characters (denote as fry_buf) strfry-ed and returned.
  • The player is expected to find fry_buf.

More importantly, the challenge server has a timeout of 20 seconds. Hence, you have to compute from the strfry-ed response in 15 seconds.

Solution⌗

Part I: The first encounter⌗

"WTF. Yet another strfry question? It must be very boring." ~ Mystiz

This is the first comment I made to the challenge. It is actually much interesting than I thought and I have spent a good 5 hours for the challenge.

The previous CTFs (for example, challenge from ångstromCTF 2020 and DawgCTF 2020) exploited on the small seed space that can be exhausted. In the previous versions of libc, the seeds for strfry is given by time(NULL) ^ getpid(). I was trying to print time(NULL) and getpid() alongside with the strfry result, but the seed does not check out. What? Maybe the world is not peaceful anymore in libc 2.31-0ubuntu9. Let's download the source code and have a read.

Part II: Code-reading game⌗

Let's verify the first point - is the implementation for strfry changed?

// string/strfry.c

char *
strfry (char *string)
{
  // omitted...
  if (!init)
    {
      static char state[32];
      rdata.state = NULL;
      __initstate_r (random_bits (),
		     state, sizeof (state), &rdata);
      init = 1;
    }
  // omitted...
}
// include/random-bits.h

static inline uint32_t
random_bits (void)
{
  struct timespec tv;
  __clock_gettime (CLOCK_MONOTONIC, &tv);
  /* Shuffle the lower bits to minimize the clock bias.  */
  uint32_t ret = tv.tv_nsec ^ tv.tv_sec;
  ret ^= (ret << 24) | (ret >> 8);
  return ret;
}

Although the string is fried in the same way, the seed is changed! Since the seed is 32 bits long, maybe I can just exhaust it. However it takes 5 seconds to strfry a 257-byte long string for 0x140000 times, it is not feasible to brute force with the challenge implementation. Let's read how random numbers are generated.

// stdlib/random_r.c

int
__initstate_r (unsigned int seed, char *arg_state, size_t n,
	       struct random_data *buf)
{
  // omitted...
  int type;
  if (n >= BREAK_3)
    type = n < BREAK_4 ? TYPE_3 : TYPE_4;
  else if (n < BREAK_1)
    {
      if (n < BREAK_0)
	goto fail;

      type = TYPE_0;
    }
  else
    type = n < BREAK_2 ? TYPE_1 : TYPE_2;

  int degree = random_poly_info.degrees[type];
  int separation = random_poly_info.seps[type];

  buf->rand_type = type;
  buf->rand_sep = separation;
  buf->rand_deg = degree;
  int32_t *state = &((int32_t *) arg_state)[1];	/* First location.  */
  /* Must set END_PTR before srandom.  */
  buf->end_ptr = &state[degree];

  buf->state = state;

  __srandom_r (seed, buf);

  state[-1] = TYPE_0;
  if (type != TYPE_0)
    state[-1] = (buf->rptr - state) * MAX_TYPES + type;
  // omitted...
}

strfry uses a 32-byte state, which indicates that TYPE_1 PRNG is used. Seven 32-bit unsigned integer is derived from the seed (denote it as s[0], s[1], ..., s[6]) and set the counter c := 0. This is the equivalent Python code.

class GlibcRandom:
    def __init__(self, seed):
        self.init_state(seed)
        [self.next() for _ in range(70)]

    def init_state(self, seed):
        state = [seed]
        for i in range(1, 7):
            h, l = seed // 127773, seed % 127773

            seed = (16807 * l - 2836 * h) & 0x7fffffff
            state.append(seed)
        self.state = [
            state,
            0
        ]
    
    def next(self):
        s, t = self.state
        v = (s[(t+3) % 7] + s[t % 7]) & 0xffffffff
        v >>= 1

        s[(t+3) % 7] += s[t % 7]
        s[(t+3) % 7] &= 0xffffffff

        self.state = [s, (t + 1) % 7]
        return v

Part III: Fast-forwarding the states⌗

Fast-forwarding the PRNG is easy. This is similar on the Team Trees challenge in CONFidence CTF this year. We can skip states with the matrix implementation (and I am able to skip the details for this part, too). After all, 5M seeds can be checked per second. Since we have only 15 seconds to recover the seed, we are unable to find the entire search space (only 1.75% of the seed space is checked). In average, we can recover the seed from the strfry output in 15 seconds once every 60 times. Finally, if we are able to recover the seed, we can freely fry and unfry strings.

After two hours, we have the flag: DrgnS{Fr13d_57r1Ng5_4r3_tH3_Be5t_s7r1NgS!}.