DiceCTF 2021 Writeup (I)

DiceCTF 2021 had an assortment of challenges and most of them are tough. Although the five crypto challenges which looked unoriginal, I was only able to solve garbled during the contest and I liked the challenges very much. After the CTF, I have found writeups from various sources and learnt a lot. In this writeup, only plagiarism and benaloh will be covered. However, I haven't look at the remaining questions yet, and they are definitely on my to-do list.

I may or may not have a part two for the remaining problems in the game, depending on my schedule and my laziness.

plagiarism⌗

Challenge Summary⌗

Seven teams ended up solving it during the contest period.

This challenge is highly referenced (or, copied) from decrypt message in RuCTF Quals 2014. In short, we are given a RSA public key: a 2048-bit $n$, $e = 1048577$ and two ciphertexts $c_1$ and $c_2$ of two related messages: $m_1 = m\ ||\ \text{``Blex''}$ and $m_2 = m\ ||\ \text{``Kane''}$. The objective is to recover $m$.

Solution⌗

I wasn't even playing CTFs in 2014 back then. However, I recalled that 2019rearrange in TetCTF 2020 had a similar idea. Suppose that we are given $e_1, e_2, u_1, u_2, c_1, c_2$ and $n$ and we are going to find $m$ satisfying $c_i \equiv (m + u_i)^{e_i}\ (\text{mod}\ n)$ for $i = 1, 2$.

The idea is rather straight forward: If we define two polynomials $p_1, p_2$ over $\mathbb{Z}_n[x]$

\[p_i(x) := (x + u_i)^{e_i} - c_i,\]

then $p_1(m) = p_2(m) = 0$. In particular, $x - m$ will be a common factor of $p_1(x)$ and $p_2(x)$. For small $e$'s, we can use Euclidean algorithm to compute GCD of polynomials. The time complexity would be $\mathcal{O}(e^2)$.

Well, @RBTree_ said that he is able to use Euclidean algorithm to solve the challenge. His solution takes 36 hours on a 144-core machine...

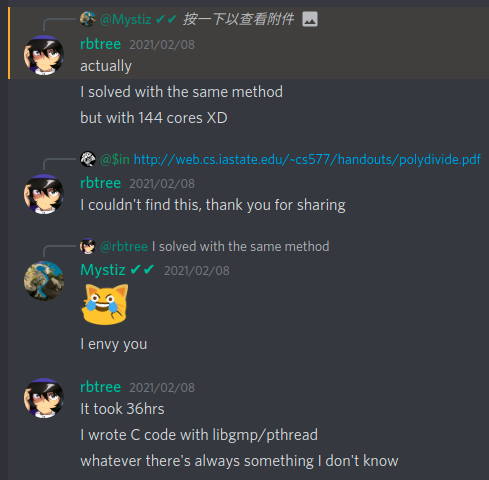
After the CTF, I learned that the existence of a faster algorithm¹ that computes GCD in $\mathcal{O}(e\log^2e)$. It is easy to implement in Sage, and I can compute the GCD in 100 minutes (for $e = 1048577$ and 2048-bit $n$).

dice{Any_sufficiently_advanced_CTF_challenge_is_indistinguishable_from_computational_number_theory}

benaloh⌗

Challenge Summary⌗

Five teams ended up solving it during the contest period.

This challenge is based on Benaloh cryptosystem with $r = 17$ and a predictable random $u$ used for encryption.

Solution⌗

This writeup is referenced from defund's writeup.

Part I: Background - Benaloh cryptosystem⌗

For anyone (including me) who is not familiar with Benaloh cryptosystem, I'll write down how the keys are generated and messages are encrypted.

Key generation⌗

Suppose that the block size is $r$, i.e., each message block is a value in $[0, r)$.

1. Pick primes $p = rp' + 1$ and $q$ such that $\gcd(p', r) = \gcd(q - 1, r) = 1$.
2. Compute $n = pq$ and $\varphi(n) = (p-1)(q-1)$.
3. Pick $0 \leq y < n$ with $y^{\varphi(n)/r} \not\equiv 1\ (\text{mod}\ n)$.
4. Compute $x = y^{\varphi(n)/r}\ \text{mod}\ n$.

The public key is $(y, n)$ and the private key is $(\varphi, x)$.

Message encryption⌗

Suppose that we want to encrypt a message $0 \leq m < r$.

1. Pick a random $0 \leq u < n$.
2. Compute $c = y^mu^r\ \text{mod}\ n$.

The ciphertext for $m$ is $c$.

Part II: What makes this challenge vulnerable⌗

The flag is broken down into 34 blocks $m_1, m_2, ..., m_{34} \in [0, 16)$, where $m_{2k-1}$ and $m_{2k}$ are derived from the $k$-th byte. We are given 34 ciphertext blocks $c_1, c_2, ..., c_{34}$. In particular, the $u$ used for the $k$-th block (denoted as $u_k$) is predictable. They are generated by a LCG and defined as $u_{k+1} = (au_k + c)\ \text{mod}\ n$ for some constants $a, c$ and $u_1 := u$. Hence,

\[c_k = y^{m_k}\left[a^ku + c(a^{k-1} + a^{k-2} + ... + 1)\right]^{17}\ \text{mod}\ n.\]

Moreover, knowing the prefix of the flag being dice{, we know $m_1, m_2, ..., m_{10}$. Hence, for $k = 1, 2, ..., 10$, we have

\[v_k := \frac{c_k}{y^{m_k}}\ \text{mod}\ n.\]

Part III: What is Gröbner basis?⌗

With the following ten congruences, is it possible to recover $a, c$ and $u$ for the LCG?

\[ \begin{cases}\begin{aligned} v_1 &\equiv u^{17} \\ v_2 &\equiv (au + c)^{17} \\ v_3 &\equiv \left[a^2u + c(a + 1)\right]^{17} \\ ... \\ v_{10} &\equiv \left[a^9u + c(a^8 + ... + a + 1)\right]^{17} \end{aligned}\end{cases}\ (\text{mod}\ n). \]

From defund's writeup, it is described that Gröbner basis is the tool we need. I searched a bit and found a YouTube video talking about it.

Suppose that we have a set of polynomials $p_1(x), p_2(x), ..., p_s(x)$ over $\mathbb{F}^k$. Let's assume that $\alpha_1, \alpha_2, ...$ are the common roots of $p_i(x) = 0$, i.e., $p_i(\alpha_k) = 0$ for all $i = 1, 2, ..., s$.

In short, Gröbner basis consists of a set of polynomials with the same common roots. Remarkably, the polynomials usually have smaller degrees.

There are more references² those I have not looked into.

Part IV: Computing a Gröbner basis⌗

I am able to compute a Gröbner basis with two minutes on my PC with the following code excerpt.

n, y = ...
cs = ...

Zn = Zmod(n)
P.<a, c, u> = PolynomialRing(Zn)

#     d___  i___  c___  e___  {____
ms = [6, 4, 6, 9, 6, 3, 6, 5, 7, 11]
vs = [c * pow(y, -m, n) % n for m, c in zip(ms, cs)]

I = ideal([
    (a^i * u + c * ((a^i - 1) // (a - 1)))^17 - vs[i]
    for i in range(10)
])

B = I.groebner_basis()
# [ u^17 + 639...272, a + 166...006, c + 275...023*u ]

We know $u^{17}$, $a$ and $\frac{c}{u}$ from the basis. It is sufficient for us to decrypt the flag, since everything on the right hand side below are known.

\[y^{-m_k} = {c_k}^{-1}{u^{17}\left[a^k + \frac{c}{u}(a^{k-1} + a^{k-2} + ... + 1)\right]^{17}}\ \text{mod}\ n.\]

dice{gr:obner!_!}