Google CTF 2021 Quals Writeup
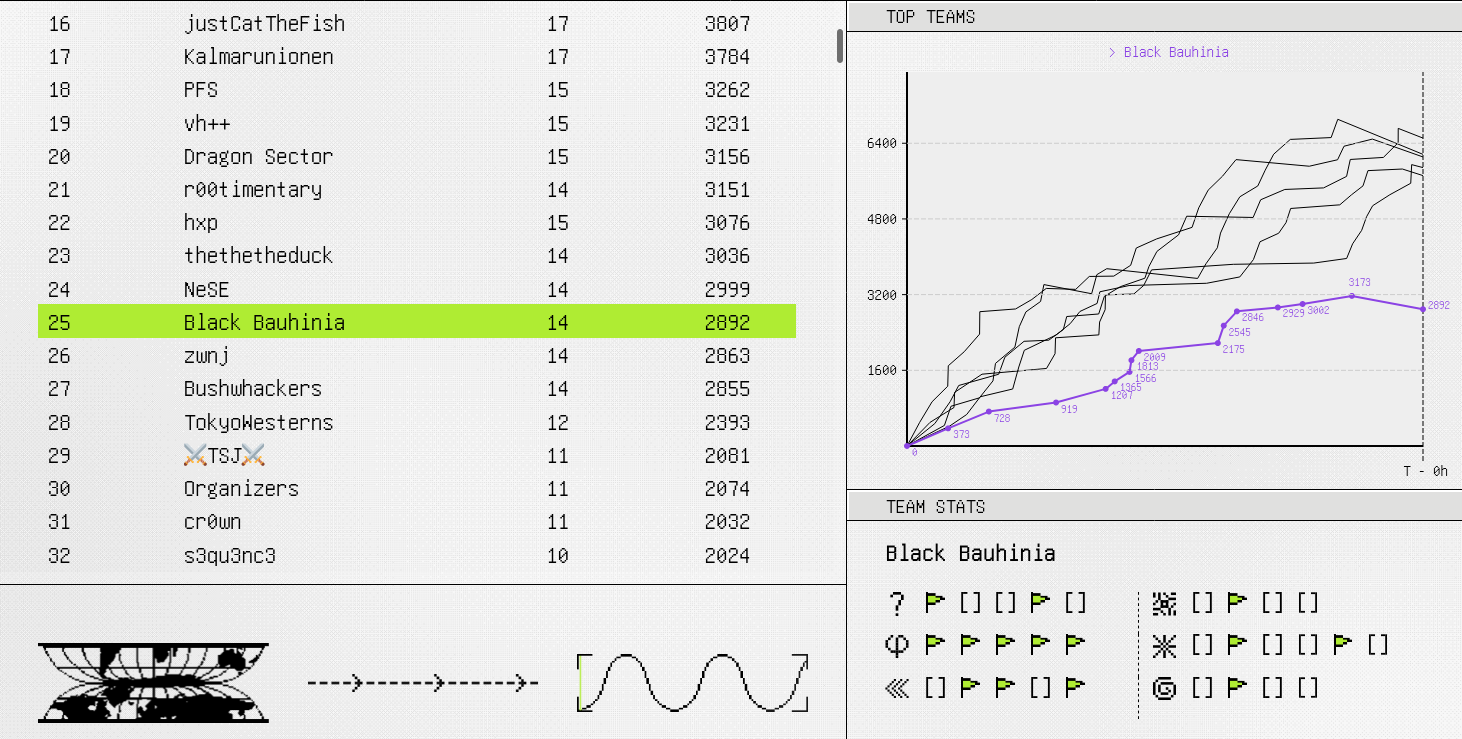
This is me playing another Google CTF with @blackb6a, ending up on the 25th place. I aced the crypto challenges and solved some challenges with my teammates. I have a strong feeling that Black Bauhinia grown a lot between the two Google CTFs and I am often backed by my teammates this time. Anyway, I will be covering all of the crypto challenges in this blog post.
H1⌗
Challenge Summary⌗
Crypto is not real hacking, they say.
Alice and Bob have a private key $d_A, d_B$ respectively and they are used for both ECDSA and ECDH. They derive a shared secret for encryption with ECDH and sign with ECDSA-SHA512.
We are given four messages those are sent between Alice and Bob (two from Alice and two from Bob). Denote the $i$-th message, ciphertext and signature being respectively $m_i$, $c_i$ and $(r_i, s_i)$ - Hereby $m_1$ and $m_3$ are signed by Alice and the rest are signed by Bob. We are given all of them except $m_3$. The objective is to recover $m_3$ where the flag is hidden.
Notably, the entropy for the RNG while generating ECDSA nonces is 128 bits long.
Solution⌗
Let's look at the source code snippets those generate the nonce.
def RNG(nbits, a, b):
nbytes = nbits // 8
B = os.urandom(nbytes)
return a * sum([B[i] * b ** i for i in range(len(B))]) % 2**nbits
# This is how they derive the nonce for ECDSA signatures
k = int(RNG(n.bit_length(), 16843009, 4294967296))From above, the nonce is in form of $k = x_0 + Ax_1 + ... + A^{15}x_{15}$, where $A = 16843009$. Hereby $0 \leq x_j < 256$ for each $j = 0, 1, ..., 15$.
Since we have two messages those are signed by Bob, it is more reasonable to find his secret key, $d$. The following are a pair of congruences those satisfied:
\[\left\{\begin{aligned} k_2 s_2 \equiv z_2 + r_2 d\ (\text{mod}\ q) \\ k_4 s_4 \equiv z_4 + r_4 d\ (\text{mod}\ q) \\ \end{aligned}\right..\]
From above, $(r_i, s_i)$ and $z_i$ are respectively the $i$-th signature and the $i$-th digest - and they are both known. On the other hand, $k_2, k_4, d$ are unknown.
We can combine the two congruences by multipling the first congruence with $r_4$ and the second with $r_2$. In that way we can eliminate one unknown $d$:
\[k_2 s_2 r_4 - k_4 s_4 r_2 \equiv z_2 r_4 - z_4 r_2\ (\text{mod}\ q).\]
Breaking down $k_2$ and $k_4$ into 16 variables: $k_i = x_{i,0} + Ax_{i,1} + ... + A^{15}x_{i,15}$, we then can proceed into the final equation:
\[\begin{aligned} s_2 r_4 x_{2,0} & + s_2 r_4 A x_{2,1} + ... + s_2 r_4 A^{15} x_{2,15} \\ & - s_4 r_2 x_{4,0} - s_4 r_2 A x_{4,1} - ... - s_4 r_2 A^{15} x_{4,15} - qy \\ & = z_2 r_4 - z_4 r_2.\\ \end{aligned}\]
From above, $0 \leq x_{i, j} < 256$ and $y \in \mathbb{Z}$. We then can use LLL to solve for $x_{i, j}$'s - hence recovering $k_i$'s and thus $d$. I have mentioned a way to solve those problems in LLL in horcrux in AeroCTF 2021 and please read that if you are interested. We have the flag after all: CTF{But_in_real_life_devs_would_never_use_such_a_buggy_RNG_right?}.
Regarding to the flag, that is definitely a no and I recalled ERC-1756 for Ethereum (which is luckily not standardized).
pythia⌗
Challenge Summary⌗
Yet another oracle, but the queries are costly and limited so be frugal with them.
A nine-letter password is split into three parts. Three keys are derived from each part of the passwords (namely $k_0, k_1, k_2$). We are given the below operations:
- Set key specifies the key $\mathcal{K} = k_i$ we will be using in the subsequent operations.
- Read flag requests the user to send the password. If it is correct, then the flag is revealed.
- Decrypt text decrypts a specified ciphertext using $\mathcal{K}$ with AES-GCM. Only return if the ciphertext is decrypted successfully.
The goal is to read the flag within 150 calls.
Solution⌗
Part I: Formulating GCM mathematically⌗
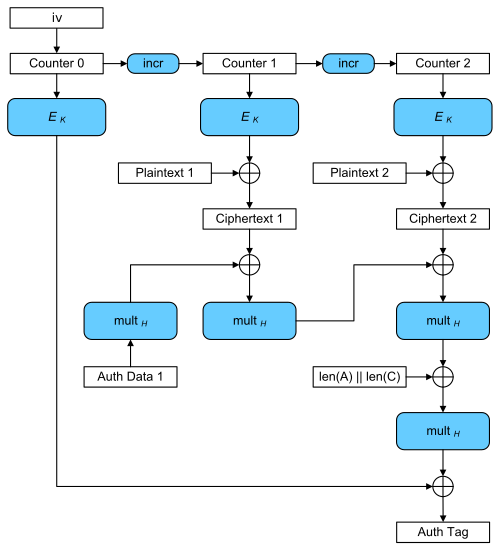
In the challenge, the authenticated data is empty. We can simply substitute Auth Data 1 in the above figure to be zero. Denote $T$ to be the authentication tag, $(C_1, C_2, ..., C_n)$ be the ciphertext blocks, $L$ be the block that specifies the length, $H := \text{Enc}(0)$ and $M := \text{Enc}(IV)$. This is an equation relating all of the variables (Note that it is operated over $\text{GF}(2^{128})$):
\[C_1 H^{n+1} + C_2 H^n + ... + C_n H^2 + LH + M = T.\]
Part II: How is the math useful?⌗
It is pretty evident that we need around 8.8K calls if we eliminate the keys one by one. That said, we should be able to eliminate many keys at once... But how?
Suppose that the $IV$ is fixed and we have $H_i := \text{Enc}_{k_i}(0)$ and $M_i := \text{Enc}_{k_i}(IV)$ for each key derived from the three character password. Let's assume that we are able to find $(C_1, C_2, ..., C_n, T)$ such that:
\[\left\{\begin{aligned} \htmlStyle{color: yellow;}{C_1} {H_1}^{n+1} + \htmlStyle{color: yellow;}{C_2} {H_1}^n + ... + \htmlStyle{color: yellow;}{C_n} {H_1}^2 + \htmlStyle{color: yellow;}{T} &= LH_1 + M_1 \\ \htmlStyle{color: yellow;}{C_1} {H_2}^{n+1} + \htmlStyle{color: yellow;}{C_2} {H_2}^n + ... + \htmlStyle{color: yellow;}{C_n} {H_2}^2 + \htmlStyle{color: yellow;}{T} &= LH_2 + M_2 \\ &... \\ \htmlStyle{color: yellow;}{C_1} {H_k}^{n+1} + \htmlStyle{color: yellow;}{C_2} {H_k}^n + ... + \htmlStyle{color: yellow;}{C_n} {H_k}^2 + \htmlStyle{color: yellow;}{T} &= LH_k + M_k \end{aligned}\right.\]
We can see that $(C_1, C_2, ..., C_n, T)$ in the $k$ equations are affine! We can solve them as a system of linear of equations. It is very likely that the solution does not fit the remaining pairs of $(H_i, M_i)$ (where $i = k+1, k+2, ...$) because there is only $1/2^{128}$ chance resulting in a false positive. We are able to eliminate $k$ possibilities if decrypt key returns a negative result, and result in $k$ possibilities otherwise.
Unfortunately, it is infeasible to play with binary search since the first step would make $k = 26^3/2$ and the complexity for solving system of linear equations is more or less $\mathcal{O}(k^3)$ - which would simply take forever.
Since we have 150 oracle calls in total and it should be generally broken down into the following procedure:
- Determine
password[0:3]within 49 oracle calls via decrypt flag. - Switch the active key to $k_1$ via set key.
- Determine
password[3:6]within 49 oracle calls via decrypt flag. - Switch the active key to $k_2$ via set key.
- Determine
password[6:9]within 49 oracle calls via udecrypt flag. - Retrieve the flag via read flag.
We need to recover $k_i$ within 49 oracle calls. In our case, we decided to employ a probabilistic approach solving the challenge.
- For the first 41 rounds, we pick 256 different keys and compute $(C_1, C_2, ..., C_n, H)$ such that the selected keys could decrypt correctly.
- If there is an decrypt text in any of the 41 rounds, then there are only 256 possible keys for $k_i$. We can use binary search to test for the correct $k_i$. This takes 8 rounds.
Note that there is a ~40% chance such that the first round would fail. That is why the approach is probabilistic.
Part III: Crowdsourcing for the Flag⌗
Now there are one problem. Since the chance for getting a flag in one go is around 20%, and it takes 25 minutes for the script to complete. Using a single instance is not a clever approach and I decided to hand the script to @harrier_lcc and @hoifanrd so that we could run the script together. They had different approaches running my script: @harrier_lcc decided to run six instances simultaneously and @hoifanrd ran a single instance.
Eventually, @hoifanrd was so lucky that he got the flag before @harrier_lcc is able to get a single byte of the password (in any of his six instances).
Apart from the drama about the fortune (and more on the misfortune), we have the flag: CTF{gCm_1s_n0t_v3ry_r0bust_4nd_1_sh0uld_us3_s0m3th1ng_els3_h3r3}.
story⌗
Challenge Summary⌗
Please, tell me a beautiful story.
When connected to the server, we are asked to send a message $m_1$ and $\text{CRC}(m_1)$ will be returned (We do not have the source code for the CRC). The server then sends a target $c_2$. The objective is to send $m_2$ such that
- $c_2 = \text{CRC}(m_2)$ and,
- the lowercase for $m_1$ is the same as the lowercase for $m_2$.
Solution⌗
It is evident that the content of $m_1$ does not matter, as long as it passes the hidden condition they impose (If the condition does not hold, it returns Your story is too short. Bye!), which I bet it is something related to the length. In our case, sending 1000 b's suffices.
Although we do not know what are the parameters for the CRC function, it is known that the function is affine. For three inputs $x, y, z$ with identical lengths, we have $\text{CRC}(x) \oplus \text{CRC}(y) \oplus \text{CRC}(z) = \text{CRC}(x \oplus y \oplus z)$.
How do we make use of this? I am presenting a not-so-efficient algorithm. To begin, we connect to the server and compute the CRCs for bbb...b, Bbb...b, bBb...b, ..., bbb...B (denote them by $m_1, r_1, r_2, ..., r_n$ and their digests by $c_1, h_1, h_2, ..., h_n$). If we are given $c_2$ asked to find a $m_2$ that satisfies the conditions stated in the challenge summary, what can we do?
Suppose that $m_2$ consists of b and B's and it has the same length of $m_1$. We can denote the indexes for B being $n_1, n_2, ..., n_k$. Then
\[m_2 = m_1 \oplus (m_1 \oplus r_{n_1}) \oplus (m_1 \oplus r_{n_2}) \oplus ... \oplus (m_1 \oplus r_{n_k}).\]
\[\begin{aligned} c_2 = \text{CRC}(m_2) &= \text{CRC}(m_1 \oplus (m_1 \oplus r_{n_1}) \oplus (m_1 \oplus r_{n_2}) \oplus ... \oplus (m_1 \oplus r_{n_k})) \\ &= \text{CRC}(m_1) \oplus \text{CRC}(r_{n_1}) \oplus \text{CRC}(m_1 \oplus (m_1 \oplus r_{n_2}) \oplus ... \oplus (m_1 \oplus r_{n_k})) \\ &= (c_1 \oplus h_{n_1}) \oplus \text{CRC}(m_1 \oplus (m_1 \oplus r_{n_2}) \oplus ... \oplus (m_1 \oplus r_{n_k})) \\ &= (c_1 \oplus h_{n_1}) \oplus \text{CRC}(m_1) \oplus \text{CRC}(r_{n_2}) \oplus \text{CRC}(m_1 \oplus (m_1 \oplus r_{n_3}) \oplus ... \oplus (m_1 \oplus r_{n_k})) \\ &= (c_1 \oplus h_{n_1}) \oplus (c_1 \oplus h_{n_2}) \oplus \text{CRC}(m_1 \oplus (m_1 \oplus r_{n_3}) \oplus ... \oplus (m_1 \oplus r_{n_k})) \\ & ... \\ &= (c_1 \oplus h_{n_1}) \oplus (c_1 \oplus h_{n_2}) \oplus ... \oplus (c_1 \oplus h_{n_k}) \oplus \text{CRC}(m_1) \\ &= (c_1 \oplus h_{n_1}) \oplus (c_1 \oplus h_{n_2}) \oplus ... \oplus (c_1 \oplus h_{n_k}) \oplus c_1 \\ \end{aligned}\]
In that case, it is equivalent to solve for $x_i$'s in $(\dagger)$:
\[(c_1 \oplus h_1) x_1 \oplus (c_1 \oplus h_2) x_2 \oplus ... \oplus (c_1 \oplus h_n) x_n = c_1 \oplus c_2 \qquad\qquad (\dagger)\]
We can construct $m_2$ with $(x_1, x_2, ..., x_n)$ and send it to the server. Then we have the flag: CTF{eb64749d08bd99b681f2bc75aa65eab35a80310f7426f6872ba869d244e37135}!
tiramisu⌗
Challenge Summary⌗
In this challenge, you establish a secure channel with the server. Good luck!
When connected to the server, it sends a ServerHello message that includes the server's public key for ECDH (on the curve P-224), as well as the flag encrypted with server's ECDH private key. We will be replying a ClientHello message that the point should be either on P-224 or P-256. We will be sending SessionMessages which is a encrypted and HMACed payload when a secure channel is established. If the HMAC is correct and the content can be correctly decrypted, the server will be responding with another SessionMessage with a slightly changed IV. The objective is to decrypt the flag.
Note that the server's key does not change upon reconnect.
Solution⌗
Part I: Invalid curve attack, but how?⌗
Since I am developing with Golang and gRPC at work, I did not spend a lot of time understanding the source code. The thing that struggled me the most is the challenge itself... Well, it was pretty evident that we are going to pick the points on P-256 and cast an invalid curve attack on P-224. However, we should pick invalid points $A$ with $A \in \mathcal{P}_{256}$ such that $qA = O$ for a small $q$. This seems difficult - and it really is!
After an uncountable amount of time, I found that I overlooked one thing: The $x$ and $y$-coordinates need not to be lying within zero and the modulus. Let $A := (x_0, y_0)$ be a point over $\mathbb{Z}_{p_{224}}$ such that $qA = O$ for some small $q$. If we pick $x$ and $y$ such that
\[\left\{\begin{aligned} &x \equiv x_G &\ (\text{mod}\ p_{256}) \\ &x \equiv x_0 &\ (\text{mod}\ p_{224}) \\ \end{aligned}\right. \qquad\text{and}\qquad \left\{\begin{aligned} &y \equiv y_G &\ (\text{mod}\ p_{256}) \\ &y \equiv y_0 &\ (\text{mod}\ p_{224}) \\ \end{aligned}\right..\]
Then $(x, y)$ is a valid point on $\mathcal{P}_{256}$ and it is also a point with small order under modulo $p_{224}$.
Part II: Invalid curve attack, but what is that?⌗
For elliptic curve Diffie-Hellman key exchange, the opposite party computes a shared secret $S$ with the formula $S := \beta A$, where $A$ is our public key and $b$ is their private key.
Suppose that we are able to find $A$ with $qA = O$ for small $q$. Then the shared secret is pretty limited - it is either $O$, $A$, $2A$, ..., $(q-1)A$.
Unfortunately, we generally cannot find such $A$s as a point on the standard curves since the curve order should be prime. To find such $A \in \mathbb{Z}_{p_{224}}^2$, we can simply generate random $b'$s and determine the order, $\rho$, of the curve $\mathcal{C}: y^2 \equiv x^3 + ax + b'\ (\text{mod}\ p_{224})$. Computing $\rho$ is a task for Sagemath. If $G$ is a generator of $\mathcal{C}$ and the $k$ is a factor of $\rho$, it implies that $A := (\rho/k) G$ satisfies $kA = O$.
Part III: Pulling off the attack⌗
In the challenge, the server is multiplying their secret key $\alpha$ to the point we gave ($A$ in our case) and its $x$-coordinate becomes the shared secret. This is a little bit different from what we had on part II. Look at the following fact:
With that said, if we send the server our forged public key ($A$, with order $q$), then we are able to find two $k\in [0, q)$ such that the $x$-coordinate of $kA$ is the shared secret. We then have $\alpha = \pm k\ (\text{mod}\ q)$.
If we have $n$ pairs of $(k_i, q_i)$'s, we are able to compute the possible values of $\alpha$ using Chinese remainder theorem. It is also important to not find small $q_i$s as the number of candidates is growing exponentially in terms of $n$.
\[\left\{\begin{aligned} \alpha &= \pm k_1\ (\text{mod}\ q_1) \\ \alpha &= \pm k_2\ (\text{mod}\ q_2) \\ & ... \\ \alpha &= \pm k_n\ (\text{mod}\ q_n) \end{aligned}\right.\]
By generating such invalid curves and computing the candidates of $\alpha$, we can eventually find the correct private key and hence the flag of the challenge: CTF{ChocolateDoesNotAskSillyQuestionsChocolateUnderstands}.
tonality⌗
Challenge Summary⌗
In this challenge, you have access to a signing oracle. Good luck!
The server generates a private key $x$ on P-256 upon connect. We are allowed to pick $\alpha$ and the server will sign $m_0$ with the private key $\alpha x$. The objective is to forge a signature for $m_1$ using the private key $x$ in a subsequent request.
Solution⌗
This is yet another ECDSA challenge in the CTF. Let's recall a condition that made the signature valid, given that $z$ is derived by the message digest, $d$ is the private key, $(r, s)$ is the signature and $k$ is a random nonce generated when signing:
\[ks \equiv z + rd\ (\text{mod}\ q)\]
Note that $k$ and $r$ are dependent to each other because $r$ is the $x$-coordinate of $k \cdot G$.
Let's formulate the whole question mathematically. Here are the steps:
- We are given two digests $z_1$ and $z_2$.
- [Sign] We are able to pick an $\alpha$ and we will be given $(r_1, s_1)$ such that $(\dagger)$ holds.
- [Forge] We send $(r_2, s_2)$ satisfying $(\dagger\dagger)$ and will be granted the flag.
\[\begin{matrix} k_1 s_1 \equiv z_1 + \alpha r_1 d\ (\text{mod}\ q) \qquad\qquad & (\dagger) \\ k_2 s_2 \equiv z_2 + r_2 d\ (\text{mod}\ q) \qquad\qquad & (\dagger\dagger) \end{matrix}\]
Since $k_1$ and $r_1$ are correlated, we rather not change any of them between the signing and the forging steps. That said, $k_1 = k_2$ and $r_1 = r_2$. With that said, $(\dagger\dagger)$ can be rewritten into $(\dagger\dagger')$.
\[k_1 s_2 \equiv z_2 + r_1 d\ (\text{mod}\ q) \qquad\qquad (\dagger\dagger')\]
Now we should think what $\alpha$ is. Since $s_2$ is the only remaining variable that we could control, we better make the right hand side for $(\dagger)$ into $z_2 + r_1d$. In that case, we can pick $\alpha = z_1 / z_2$.
\[k_1 s_1 \equiv z_1 + \frac{z_1}{z_2} r_1 d\ (\text{mod}\ q) \qquad\qquad (\dagger')\]
Multiplying both sides of $(\dagger')$ by $z_2 / z_1$, we then have
\[k_1 \frac{s_1z_2}{z_1} \equiv z_2 + r_1 d\ (\text{mod}\ q) \qquad\qquad (\dagger'')\]
Comparing $(\dagger'')$ and $(\dagger\dagger')$, we can see that $s_2 = s_1z_2 / z_1$.
With the idea implemented, we have the flag: CTF{TheySayTheEmptyCanRattlesTheMost}.