LagLeg is a crypto challenge in ASIS CTF Quals 2021. We are asked to factor a given $n$ with $n = (r^5 + s)(r + s)$ as part of the challenge. Hereby $r$ and $s$ are respectively 256 and 64 bits long. I think my approach used is very unique and creative - and definitely worth mentioning. It does not mean that it is a good approach, however.

I will record the exact steps I solved the challenge. However, I will update the bounds and prove the whole thing so that it looked more rigorous. The full code will be attached at the end of the blog post, too.

The sizes of $r$ and $s$ are wrong! The organizers have reiterated that $r$ and $s$ should be 128 and 32 bits long. I was too late to notice the announcement and solved the harder version (i.e., the one with larger parameters). The nerfed one can be factorized by brute-forcing $s$, which is not fun.

Problem Statement⌗

Suppose that $r \in [2^{255}, 2^{256})$ and $s \in [2^{63}, 2^{64})$. Suppose also $p = r^5 + s$ and $q = r + s$ are primes. Factorize $n := pq$.

Solution⌗

We will denote $\hat{r_k}$ be an estimate of $r$ and $\Delta r_k := r - \hat{r_k}$. As an example, we will use the below parameters freshly generated from the challenge script:

r = 113998029782126404385159208354017152656462126437187882248430209727665881104644
s = 11008047941767198067

Part I: Estimating $r$ with a 64-bit error⌗

We can easily spot that $r \approx n^{1/6}$ since $n = r^6 + r^5s + rs + s^2 \approx r^6$. Hence, let's denote $\hat{r_1} = \lfloor n^{1/6} \rfloor$ be an estimate of $r$.

Theorem 1. $-2^{64} \leq \Delta r_1 \leq 0$.

Proof.

\[\begin{aligned} & n = (r^5 + s)(r + s) \\ \Longrightarrow &\ r^6 = r^5 \cdot r < n < (r + s)^5 (r + s) = (r + s)^6 < (r + 2^{64})^6 \\ \Longrightarrow &\ r < n^{1/6} < r + 2^{64} \\ \Longrightarrow &\ r \leq \hat{r_1} \leq r + 2^{64} \\ \Longrightarrow &\ r \leq r - \Delta r_1 \leq r + 2^{64} \\ \Longrightarrow &\ -2^{64} \leq \Delta r_1 \leq 0 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \blacksquare \end{aligned}\]

Current progress for the example. $\Delta r_1 = -1834674656961199677 \approx -2^{61}$.

Part II: Reducing the error of $r$ to 38 bits⌗

We could also show that $n\ \text{mod}\ r = s^2$. Since $s^2$ is 128-bit long but $r$ itself is of 256 bits, this got me thinking: Could we detect that our estimate $\hat{r}$ is close to $r$? Turns out we can. Under modulo $\hat{r}$, we have

\[n \equiv [(\hat{r} + \Delta r)^5 + s] [(\hat{r} + \Delta r) + s] \equiv (\Delta r^5 + s)(\Delta r + s) \equiv \Delta r^6 + \Delta r^5 s + \Delta r s + s^2 \ (\text{mod}\ \hat{r}).\]

Theorem 2A. Suppose that $s \in [0, 2^{64})$. If $\Delta r \in [-s^{1/5}, 2^{38})$, then the below equation holds (note that this is not a modular equation):

\[n\ \text{mod}\ \hat{r} = \Delta r^6 + \Delta r^5 s + \Delta r s + s^2.\]

Proof.

(1) Lower Bound

\[\Delta r^6 + \Delta r^5 s + \Delta r s + s^2 = (\Delta r^5 + s)(\Delta r + s) \geq [(-s^{1/5})^5 + s][-s^{1/5} + s] = 0\]

(2) Upper Bound

\[\begin{aligned} \Delta r^6 + \Delta r^5 s + \Delta r s + s^2 &< (2^{38})^6 + (2^{38})^5 \cdot 2^{64} + 2^{38} \cdot 2^{64} + (2^{64})^2 \\ & = 2^{228} + 2^{254} + 2^{102} + 2^{128} = 2^{254} + (2^{228} + 2^{128} + 2^{102}) \\ & < 2^{254} + 2^{254} = 2^{255} \leq \hat{r} \end{aligned}\]

Therefore $0 \leq \Delta r^6 + \Delta r^5 s + \Delta r s + s^2 < \hat{r}$. Also $n \equiv \Delta r^6 + \Delta r^5 s + \Delta r s + s^2 \ (\text{mod}\ \hat{r})$, thus

\[n\ \text{mod}\ \hat{r} = \Delta r^6 + \Delta r^5 s + \Delta r s + s^2. \qquad \blacksquare\]

Theorem 2B. Suppose that $s \in [0, 2^{64})$. If $\Delta r \in [-2^{38}, -s^{1/5})$, then:

\[n\ \text{mod}\ \hat{r} = \Delta r^6 + \Delta r^5 s + \Delta r s + s^2 + \hat{r}.\]

Proof.

(1) Lower Bound

\[\begin{aligned} \Delta r^6 + \Delta r^5 s + \Delta r s + s^2 &= (\Delta r^5 + s)(\Delta r + s) > [(-2^{38})^5 + s](-2^{38} + s) \\ & = -(2^{190} - s)(s - 2^{38}) > -2^{190} \cdot (2^{64} - 2^{38}) \\ & > -2^{190} \cdot 2^{64} = -2^{254} > -\hat{r} \end{aligned}\]

(2) Upper Bound

\[\Delta r^6 + \Delta r^5 s + \Delta r s + s^2 = (\Delta r^5 + s)(\Delta r + s) < [(-s^{1/5})^5 + s][-s^{1/5} + s] = 0\]

Thus $-\hat{r} \leq \Delta r^6 + \Delta r^5 s + \Delta r s + s^2 < 0$. Using a similar argument as Theorem 2A, we have

\[n\ \text{mod}\ \hat{r} = \Delta r^6 + \Delta r^5 s + \Delta r s + s^2. \qquad \blacksquare\]

Theorem 3.

If $\Delta r \in [2^{38}, -s^{1/5}-1) \cup [-s^{1/5}, 2^{38}-1)$, then

\[[n\ \text{mod}\ \hat{r}] - [n\ \text{mod}\ (\hat{r} + 1)] \approx 5 \Delta r^4 s.\]

Proof.

From Theorem 2A, if $\Delta r \in [-s^{1/5}, 2^{38}-1)$, we can compute

\[\begin{aligned} & [n\ \text{mod}\ \hat{r}] - [n\ \text{mod}\ (\hat{r} + 1)] \\ & = [\Delta r^6 + \Delta r^5 s + \Delta r s + s^2] - [(\Delta r - 1)^6 + (\Delta r - 1)^5 s + (\Delta r - 1)s + s^2] \\ & = -\sum_{k=0}^5 {6 \choose k} (-1)^{6 - k} \Delta r^k - \sum_{k=0}^4 {5 \choose k} (-1)^{6 - k} \Delta r^k s - s \\ & \approx 6 \Delta r^5 + 5 \Delta r^4 s - s \\ & \approx 5 \Delta r^4 s \end{aligned}\]

Similarly, we could apply Theorem 2B on the interval $[2^{38}, -s^{1/5}-1)$ and obtain the same result. Omitted. $\blacksquare$

The above quantity would be approximately 216 bits long if $\Delta r$ is 38 bits long. This is significantly smaller than $\hat{r}$. That said, we could exhaust $k \in [0, 2^{25})$ and define $\hat{r_2} := \hat{r_1} - 2^{39} k$. There exists a $k$ such that $\Delta r_2 \in [-2^{38}, 2^{38})$.

Current progress for the example. $\Delta r_2 = -131959783875 \approx -2^{37}$.

Part III: Reducing the error of $r$ to 13 bits⌗

Mystiz' postmortem. This part is my motivation to compile the entire blog post. While I am writing the blog post, I thought of some different ways (to be verified!) which might look better.

When $r \in [-s^{1/5}, 2^{38})$, it is not hard to show that either $n\ \text{mod}\ \hat{r}$ is either dominated by the term $\Delta r^5 s$ or $s^2$. The below chart shows a relationship between the average number of bits for $n\ \text{mod}\ \hat{r}$ (the $y$-axis) with respect to the number of bits of $\Delta r$ (the $x$ axis). When $x < 0$, the number of bits for $\Delta r < 0$ would be $-x$ bits instead.

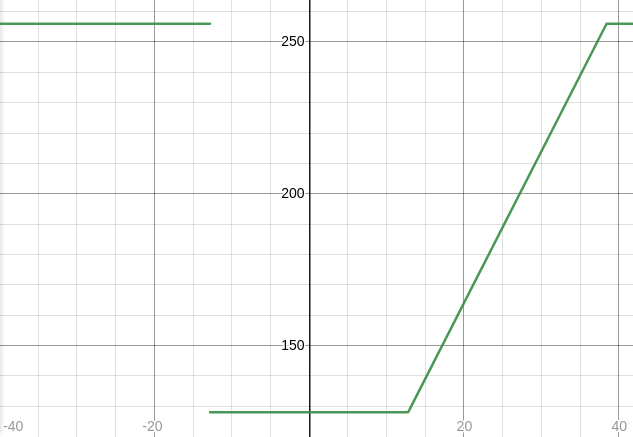
Average number of bits for $n\ \text{mod}\ \hat{r}$ ($y$) when $\Delta r$ is $x$ bits long.

We can see that the curve is somehow convex. In particular, the minimum is reached (128 bits) when $\left| \Delta r \right| < 2^{13}$. I used ternary search, an algorithm to find a minimum in a convex function (resp. a maximum in a concave function), to find a smaller $\Delta r$.

Current progress for the example. $\Delta r_3 = 6426 \approx 2^{13}$.

Part IV: Recovering the $r$⌗

Since $r \in [\hat{r_3} - 2^{13}, \hat{r_3} + 2^{13}]$, we can exhaust them. Since $n\ \text{mod}\ r = s^2$, for each $\hat{r_4}$ compute $s := \sqrt{n\ \text{mod}\ \hat{r_4}}$. We can simply skip it if $s$ is not integral. We can check $n = (\hat{r_4}^5 + s)(\hat{r_4} + s)$ and this is the factorization if that holds.

Current progress for the example. $\Delta r_4 = 0$. 🎉

Full Script of Demo⌗ 

DEBUG = True

if DEBUG:
    # You could supply us a set of r, s and we will show you the difference to the real r between rounds
    r = 113998029782126404385159208354017152656462126437187882248430209727665881104644
    s = 11008047941767198067

    p = r**5 + s
    q = r + s
    n = p*q
else:
    # ...or simply supply a n and factorize!
    n = 2194745024596516930061246071521532383749440430915141363754761092243619425670778331059219910671541483862140532961743221108780498988042304929562381481533407394601822343368834886452526191822249795788174976999385462863764483817025176363119720182456801645579673261861976948637579703389499297187098811992421871026864635570228942497268726757914152423140637424251871294427010392263487971250800024725318581331293235687094301490549921462929374203575935128381396777573430901

# ===


# PART I

from gmpy2 import iroot
r1_hat, _ = iroot(n, 6)
r1_hat = int(r1_hat)

print(f'r1_hat = {r1_hat}')
if DEBUG:
    delta_r1 = r - r1_hat
    print(f'delta_r1 = {delta_r1}')
    print(f'delta_r1.bit_length() = {delta_r1.bit_length()}')

# PART II

from tqdm import tqdm
min_y, min_k = n, 0
W = 2**39
for k in tqdm(range(2**25)):
    r2_hat = r1_hat - 2**39 * k
    y = (n % r2_hat) - (n % (r2_hat + 1))

    if 0 <= y < min_y:
        min_y, min_k = y, k
            
r2_hat = r1_hat - 2**39 * min_k

print(f'r2_hat = {r2_hat}')
if DEBUG:
    delta_r2 = r2_hat - r
    print(f'delta_r2 = {delta_r2}')
    print(f'delta_r2.bit_length() = {delta_r2.bit_length()}')


# PART III

lb, ub = r2_hat - 2**38, r2_hat + 2**38

while lb + 10 < ub:
    llb = (2*lb + ub) // 3
    uub = (lb + 2*ub) // 3

    if n % llb > n % uub:
        lb = llb
    else:
        ub = uub

r3_hat = lb
print(f'r3_hat = {r3_hat}')
if DEBUG:
    delta_r3 = r3_hat - r
    print(f'delta_r3 = {delta_r3}')
    print(f'delta_r3.bit_length() = {delta_r3.bit_length()}')

# PART IV

from gmpy2 import iroot
for k in range(-2**13, 2**13):
    r4_hat = r3_hat + k
    s, ok = iroot(n % r4_hat, 2)
    if not ok: continue
    s = int(s)
    if n == (r4_hat**5 + s) * (r4_hat + s): break
else:
    assert False, "cannot factor n"

print(f'r4_hat = {r4_hat}')
if DEBUG:
    delta_r4 = r4_hat - r
    print(f'delta_r4 = {delta_r4}')
    print(f'delta_r4.bit_length() = {delta_r4.bit_length()}')