MOCSCTF 2022 Postmortem
@blackb6a helped preparing some challenges for MOCSCTF, a 8.5-hour long CTF in Macau. This time I wrote nine challenges and @hoifanrd made one of them (3-AES). This blog post covers the intended solution for all of them.
These are the summary of the challenges:
| Challenge Name | Category | Solves |
|---|---|---|
| RSA Trio | Crypto | 2/43 |
| Slightly Informative | Crypto | 2/43 |
| NP-SHA256 | Crypto | 1/43 |
| HMAC-SHA256 | Crypto | 2/43 |
| RC4 | Crypto | 0/43 |
| HashTable | Misc | 3/43 |
| Wordle | Crypto, Misc | 0/43 |
| 3-AES | Crypto, Misc | 0/43 |
| Elementary | Reverse | 0/43 |
| Redactor | Reverse | 1/43 |
RSA Trio (Crypto)⌗
Challenge Summary⌗
RSA is difficult. What if Rivest, Shamir and Adleman encrypt your message together?
nc HOST PORTAttachments: chall.py
When connected to the server, three 1024-bit primes $p$, $q$ and $r$ are generated. Let $n_1 = pq$, $n_2 = qr$ and $n_3 = rp$ and three RSA public keys $(n_1, e)$, $(n_2, e)$, $(n_3, e)$ are constructed (here e = 0b10001 and $q < p < r$, i.e., $n_1 < n_2 < n_3$).
Let $\mathcal{E}(m)$ be the encryption function that returns the ciphertext $c$:
\[\begin{aligned} & t_1 = m^e\ \text{mod}\ n_1 \\ & t_2 = {t_1}^e\ \text{mod}\ n_2 \\ & c = {t_2}^e\ \text{mod}\ n_3. \end{aligned}\]
Long story short: the message is encrypted with the RSA public keys in order. Also, if $m \not\in [0, n_1)$, $t_1 \not\in [0, n_2)$ or $t_2 \not\in [0, n_3)$, nothing will be returned.
We are allowed to call the encryption function $\mathcal{E}$ for an arbitrary amount of times and are given $\mathcal{E}(\text{flag})$ at the very beginning. The goal is to recover the flag.
Solution⌗
Recovering $n_1$⌗
Since $t_1 = m^e\ \text{mod}\ n_1 \in [0, n_1) \subset [0, n_2)$, it is impossible that $t_1 \not\in [0, n_2)$. Likewise it is always true that $t_2 \in [0, n_3)$. That said, we can get a ciphertext of $m$ if and only if $m \in [0, n_1)$. Since $0 \leq n_1 < 2^{2048}$, we can recover $n_1$ via binary search calling $\mathcal{E}$ 2048 times.
Recovering $n_3$⌗
This part is easier. We must observe that e = 0b10001 (instead of e = 0x10001), which makes $e = 17$. For we send $m$ with $0 \leq m^{289} < n_2$ but $m^{4913} \geq n_3$, then $t_1 = m^{17}$ and $t_2 = m^{289}$ (not taken modulo) and $c = m^{4913}\ \text{mod}\ n_3$. This implies that $c$ is the remainder when $m^{4913}$ is divided by $n_3$. Well, $m = 2$ and $m = 3$ are such values. We can recover a small multiple of $n_3$ by
\[k \cdot n_3 := \gcd\left(2^{4913} - \mathcal{E}(2), 3^{4913} - \mathcal{E}(3)\right).\]
We can easily recover $n_3$ from $k$ by testing if they are divisible by small primes.
Finishing the challenge⌗
From here, we obtain $n_1 = pq$ and $n_3 = rp$. We can recover $p$ by $p := \gcd(n_1, n_3)$, thus effectively recover $q = n_1 / p$ and $r = n_3 / p$. We will obtain private exponents $d_1$, $d_2$ and $d_3$, allow us to decrypt the flag.
MOCSCTF{shar1n9_pr1m3s_f0r_r5a_1s_n0t_4_sm4r7_m0v3}Slightly Informative (Crypto)⌗
Challenge Summary⌗
What will happen if I am giving some more information about my RSA key?
Attachments: chall.py, output.txt
We are given a RSA public key $(n, e)$ with $n = pq$ and a encrypted flag $c$. We are also given $s$ and $t$ such that $d = sp + t$ ($d$ is the private exponent). The objective is to recover the flag.
n = 104761374953173292488929744863165210794654068795777885288141577481002622221368522222345141465054888216685195323019389786561685227925970380642821816770602985472200153940453825122714968250922188816858014096712757866955919806714643962473332876738158067418215518151671679136192434497079441504252290233276785611599
e = 65537
c = 65928964054587881283125968144498292857628864173177955118556976763155079656459679077792117840779590338576427244089037717506889027748698067761926112680228885555444571382015302945365206338671155793788123643640188995655372264100530540193424123290247632274913224252938261740392478884552717293366009033122985923910
s = 5142613903784744424286082317496829116877907073407033860339838239164453521174213069438631369864823275015906330523317080155171707469704307761287329022024572
t = 7967501076725747803058232903884621217031867311480596291389476854702834454579805205282313799601751011483434096767204486104203547013606991412953137405179501Solution⌗
To begin, we will recall how the private exponent $d$ is defined:
\[e \cdot d \equiv 1 \ (\text{mod}\ \phi(n)).\]
If we replace $\phi(n) = (p - 1)(q - 1)$ remove the use of modular equation, we can see that there exists a non-negative integer $k$ such that
\[e \cdot d = 1 + k(p - 1)(q - 1) = k[(n + 1) - (p + q)].\]
Let's substitute $d = sp + t$ so that is an equation of three unknowns: $p, q$ and $k$.
\[e (sp + t) = 1 + k[(n + 1) - (p + q)]\]
We can further eliminate the unknown $q$ because $pq = n$.
\[\begin{aligned} & e (sp + t) = 1 + k[(n + 1) - (p + n/p)] \\ \Longrightarrow \quad & es \cdot p^2 + et \cdot p = p + k(n + 1) \cdot p - k \cdot p^2 - kn \\ \Longrightarrow \quad & (k + es) \cdot p^2 + [et - 1 - k(n+1)] \cdot p + kn = 0 \qquad [\dagger] \end{aligned}\]
What we see is a quadratic equation in $p$. But guess what? $k$ is another unknown so what I said is not exactly true. Here comes one more fact:
\[\begin{aligned} & e \cdot d = 1 + k \cdot \phi(n) > k \cdot \phi(n) \\ \Longrightarrow \quad & \frac{k}{e} < \frac{d}{\phi(n)} = 1 \\ \Longrightarrow \quad & k < e = 65537. \end{aligned}\]
Because $k$ is also non-negative, $k$ could only be 0, 1, ..., or $e-1$. As there are only 65537 possibility, we can exhaust every $k$ into $[\dagger]$. Now we can solve 65537 quadratic equations and test every root $p$ obtained. That said, if $p$ is a positive integer such that $n$ is divisible by $p$, then we are able to factorize $n = pq$.
Eventually, we can compute $\phi(n) = (p - 1)(q - 1)$ and compute $d = e^{-1}\ \text{mod}\ \phi(n)$. We can use the private exponent to recover the flag:
MOCSCTF{st0p_l34k1ng_3x7r4_5tuffs_ab0u7_y0ur_r5a_k3y}
Postmortem. sahuang from team Project SEKAI has an alternate solution, which is pretty elegant:
Since $e \cdot d \equiv 1\ (\text{mod}\ \phi(n))$, we also have $e \cdot d \equiv 1\ (\text{mod}\ (p-1))$ which lead to
$$e \cdot (sp + t) \equiv 1\ (\text{mod}\ (p-1)) \Longrightarrow e \cdot (s + t) \equiv 1\ (\text{mod}\ (p-1)).$$
That said, $p - 1$ is a factor of $M := e \cdot (s + t) - 1$. To be accurate, $M$ is a small multiple of $p - 1$. We can factor $M$ from factordb and obtain $p$, thus factoring $n$ as well.
NP-SHA256 (Crypto)⌗
Challenge Summary⌗
I have copied a SHA-256 implementation available online while having the padding removed. It is now 0.1% faster without having the security premises broken.
nc HOST PORT
The challenge copies a Python SHA256 implementation from keanemind/Python-SHA-256 with few lines removed:
def generate_hash(message: bytearray) -> bytearray:
# (omitted)
# Padding
length = len(message) * 8 # len(message) is number of BYTES!!!
message.append(0x80)
- while (len(message) * 8 + 64) % 512 != 0:
- message.append(0x00)
-
- message += length.to_bytes(8, 'big') # pad to 8 bytes or 64 bits
-
- assert (len(message) * 8) % 512 == 0, "Padding did not complete properly!"
# Parsing
blocks = [] # contains 512-bit chunks of message
for i in range(0, len(message), 64): # 64 bytes is 512 bits
blocks.append(message[i:i+64])The objective is to find a hash collision of the patched SHA256, i.e., find $m_1$ and $m_2$, at least 64-byte long, such that $m_1 \neq m_2$ and $\text{SHA256}(m_1) = \text{SHA256}(m_2)$.
Solution⌗
The solution is simple: Let $m_1$ and $m_2$ be the messages with 64 null bytes and 65 null bytes, respectively. Then $\text{SHA256}(m_1) = \text{SHA256}(m_2)$.
[>] 00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
[>] 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
[<] Good! MOCSCTF{ev3ry_d3t41l_1n_cryp70gr4phy_m4t73rs}But why? Let's compute $\text{SHA256}(m_3)$ and $\text{SHA256}(m_4)$, where $m_3$ and $m_4$ are the empty message and the message with one null byte respectively:
m3 = bytes.fromhex('')
m4 = bytes.fromhex('00')Let's copy the generate_hash function to explain the stuffs. I have innotate the stuffs with comments:
def generate_hash(message: bytearray) -> bytearray:
"""Return a SHA-256 hash from the message passed.
The argument should be a bytes, bytearray, or
string object."""
if isinstance(message, str):
message = bytearray(message, 'ascii')
elif isinstance(message, bytes):
message = bytearray(message)
elif not isinstance(message, bytearray):
raise TypeError
# Padding
length = len(message) * 8
message.append(0x80)
# [MYSTIZ'S COMMENT]
# At this stage,
# message = bytes.fromhex("80") # -- for m3
# message = bytes.fromhex("0080") # -- for m4
blocks = []
for i in range(0, len(message), 64): # 64 bytes is 512 bits
blocks.append(message[i:i+64])
# [MYSTIZ'S COMMENT]
# At this stage,
# blocks = [bytes.fromhex("80")] # -- for m3
# blocks = [bytes.fromhex("0080")] # -- for m4
h0 = 0x6a09e667
h1 = 0xbb67ae85
h2 = 0x3c6ef372
h3 = 0xa54ff53a
h5 = 0x9b05688c
h4 = 0x510e527f
h6 = 0x1f83d9ab
h7 = 0x5be0cd19
# [MYSTIZ'S COMMENT]
# Since there is only one block, I'll rewrite below without losing the meaning:
message_block = blocks[0]
message_schedule = []
for t in range(0, 64):
if t <= 15:
message_schedule.append(bytes(message_block[t*4:(t*4)+4]))
# [MYSTIZ'S COMMENT]
# At this stage,
# message_schedule[0] = bytes.fromhex("80") # -- for m3
# message_schedule[0] = bytes.fromhex("0080") # -- for m4
# and for i = 1, 2, ..., 15
# message_schedule[i] = b"" # for both m3 and m4
else:
term1 = _sigma1(int.from_bytes(message_schedule[t-2], 'big'))
term2 = int.from_bytes(message_schedule[t-7], 'big')
term3 = _sigma0(int.from_bytes(message_schedule[t-15], 'big'))
term4 = int.from_bytes(message_schedule[t-16], 'big')
schedule = ((term1 + term2 + term3 + term4) % 2**32).to_bytes(4, 'big')
message_schedule.append(schedule)
# [MYSTIZ'S COMMENT]
# For i = 16, 17, ..., 64, message_schedule[i] for m3 and m4 are equal.
# This is because that the big-endian representations for
# bytes.fromhex("80") and bytes.fromhex("0080") are the same.
assert len(message_schedule) == 64
# (omitted)
for t in range(64):
t1 = ((h + _capsigma1(e) + _ch(e, f, g) + K[t] +
int.from_bytes(message_schedule[t], 'big')) % 2**32)
# [MYSTIZ'S COMMENT]
# t1 on the i-th round looks for the big-endian representation for
# message_schedule[i]. That said, t1 for m3 and m4 would always be the same.
# After all, this makes a, b, ..., h for both m3 and m4 equal for each round.
# (omitted)
# [MYSTIZ'S COMMENT]
# Now h0, h1, ..., h7 for both m3 and m4 are equal.
# That would imply the digests would be the same.
h0 = (h0 + a) % 2**32
h1 = (h1 + b) % 2**32
h2 = (h2 + c) % 2**32
h3 = (h3 + d) % 2**32
h4 = (h4 + e) % 2**32
h5 = (h5 + f) % 2**32
h6 = (h6 + g) % 2**32
h7 = (h7 + h) % 2**32
return ((h0).to_bytes(4, 'big') + (h1).to_bytes(4, 'big') +
(h2).to_bytes(4, 'big') + (h3).to_bytes(4, 'big') +
(h4).to_bytes(4, 'big') + (h5).to_bytes(4, 'big') +
(h6).to_bytes(4, 'big') + (h7).to_bytes(4, 'big'))It is essentially the same for $m_1$ and $m_2$, except the initial values $h_0, h_1, ..., h_7$ are different. Let's leave that as readers' exercise.
HMAC-SHA256 (Crypto)⌗
Challenge Summary⌗
It is advised to solve NP-SHA256 first. Does it help? I freakly don't know.
nc HOST PORTAttachments: chall.py
We are asked to find 64 pairs of $(k, m)$ such that $\text{HMAC-SHA256}_k(m)$ are all equal.
Solution⌗
When the key is shorter than the block size (64 for SHA256), it will be padded by zeros on the right.1 For example, if the key is hello world, then it will be padded to hello world_____________________________________________________ (hereby each _ represents a null byte). It is easy to see that the keys foo and foo_ would be padded into the same key, thus generating equal hashes for equal messages.
After all, the below 65 keys would be padded into the same way:
- an empty key
_(one null byte)__(two null bytes)___(three null bytes)
...________________________________________________________________(64 null bytes)
and they all generate equal hashes given the same message. By sending such keys to the server (for an arbitrary message), we can obtain the flag:
MOCSCTF{wh4t_i5_th3_u53_0f_5uch_c0111si0ns_w1th_d1ff3ren7_k3y5}RC4 (Crypto)⌗
Challenge Summary⌗
There are many attacks for RC4 on the internet. Maybe you can find one and apply on this challenge (or not).
nc HOST PORTAttachments: chall.py
When connected to the server, a 16-byte key will be generated for an altered RC4. We can call the below functions for an arbitrary number of times:
- [Encrypt message] Send $m$ and obtain $\text{RC4}(m)$,
- [Encrypt flag] Obtain $\text{RC4}(\text{flag})$.
The objective is to obtain the flag.
class RC4:
def __init__(self, key):
keylength = len(key)
s = [i for i in range(256)]
j = 0
for i in range(256):
j = (j + s[i] + key[i % keylength]) % 0xff
s[i], s[j] = s[j], s[i]
self.i = 0
self.j = 0
self.s = s
def __next(self):
s, i, j = self.s, self.i, self.j
i = (i + 1) % 0xff
j = (j + s[i]) % 0xff
s[i], s[j] = s[j], s[i]
self.s, self.i, self.j = s, i, j
return s[(s[i] + s[j]) % 0xff]
def encrypt(self, message):
return bytes(m^self.__next() for m in message)Solution⌗
What's wrong with the RC4 function?⌗
The RC4 function is not implemented correctly. We can either observe this by
- comparing ciphertexts of an existing and the current RC4 implementations, or
- reading the source code carefully.
We can see that the error comes from % 0xff, which should be & 0xff (or % 256, which is the same).
Exploiting the mistake⌗
By taking everything modulo 255, the indexes for s is always between $[0, 255)$. Thus s[255] is never accessed in the __next function. That said, s[255] (we will use $x$ below) would never be used in the keystream.
We can encrypt a bunch of null bytes and obtain the keystream bytes $(k_1, k_2, ..., k_n)$. If the set $\{k_1, k_2, ..., k_n\}$ has 255 elements, we can effectively recover $x$. After that, we can repeatedly obtain $\text{RC4}(\text{flag})$. If $y$ never appears in the $i$-th byte of $\text{RC4}(\text{flag})$, then $x \oplus y$ is the $i$-th byte of the flag (i.e., the plaintext). We can obtain the flag by working on this on every character:
MOCSCTF{i_sh0uld_u5e_AND_0xff_in5t3ad_0f_M0D_0xff}HashTable (Misc)⌗
Challenge Summary⌗
Making CTF challenges is easy -- Copy code from Github, make it vulnerable and the challenge is done. Mystiz has copied a HashTable implementation and it is your turn to read the flag.
nc HOST PORTAttachments: chall.py, hashtable.py
We are given a Python implementation of hash table. There is a server that allows us to interact with the hash table ($k_0$ is a 16-byte secret):
- [Set] Given $k$ and $v$, sets $\text{HashTable}[k] := v$.
- [Get] Given $k$, gets $\text{HashTable}[k]$.
- [Delete] Given $k$, removes $\text{HashTable}[k]$.
- [Put secret] Sets $\text{HashTable}[k_0] := \text{no flag for you}$.
- [Get secret] If $\text{HashTable}[k_0] \neq \text{no flag for you}$ then we are given the flag (we need to call put secret at least once).
Solution⌗
There are at least two bugs of the implementation:
- If the key $\hat{k}$ is on the first of the bucket, then all entries from the same bucket will be removed upon $\text{Delete}(\hat{k})$.
- Suppose that $\text{HashTable}[\hat{k}] = v_1$. Calling $\text{Set}(\hat{k}, v_2)$ would not make the subsequent calls of $\text{Get}(\hat{k})$ to return $v_2$ (i.e., the key is not overwritten).
We will use the first bug to remove $\text{HashTable}[k_0]$ without knowing what $k_0$. Assume that $k_0$ maps to the $b$-th bucket. We can retrieve the flag with the below steps:
- Find a key $k_1$ that also maps to the $b$-th bucket.
- Call $\text{Set}(k_1, \text{whatever})$ to occupy the first slot of the $b$-th bucket.
- Call $\text{PutSecret}$, which puts the secret in the second slot of $b$-th bucket.
- <🐞> Call $\text{Delete}(k_1)$ to remove all of the entries from the $b$-th bucket. That said $\text{HashTable}(k_0)$ is accidentally removed.
- Call $\text{GetSecret}$. Since $\text{HashTable}[k_0]$ removed, $\text{HashTable}[k_0] \neq \text{no flag for you}$ and thus we have the flag.
To solve the challenge, we simply occupy the first slot of all buckets in step 2 and remove all of the entries in step 4. Eventually we have the flag:
MOCSCTF{wr1t3_un1t_t3st5_f0r_y0ur_s4n1ty}Wordle (Crypto, Misc)⌗
Challenge Summary⌗
You can guess the word in five attempts. But can you guess the word in ONE attempt?
nc HOST PORTAttachments: chall.py
We are given a server that plays Wordle with us. The words are picked randomly from the Random class defined below (which is a linear congruential generator):
class Random:
def __init__(self):
self.seed = random.getrandbits(128)
self.multiplier = 271828182845904523536028
self.increment = 314159265358979323846264
self.modulus = 246024225711064289902592
def next(self):
self.seed = (self.seed * self.multiplier + self.increment) % self.modulus
return self.seedWe can play up to fifty games if we don't lose a game. More importantly, the goal is to guess the word in the first time for ten consecutive games.
Solution⌗
Playing Wordle⌗
Having a strategy of playing Wordle is now a survival skill. Since there are a lot of blog posts and resources online, I am not going to explain it in my way. These are some interesting ones:
- Maximising Differential Entropy to Solve Wordle by Aditya Sengupta (Link)
- Unwordle by sadmoody (Link)
- Absurdle by qntm (Link)
- Solving Wordle using information theory by 3Blue1Brown (Link)
Analysing the Random class⌗
The $n$-th number, $x_n$, outputed from the PRNG will be
\[x_n = \begin{cases} (a x_{n-1} + b)\ \text{mod}\ m & \text{if}\ n > 0 \\ \text{seed} & \text{if}\ n = 0 \end{cases},\]
where $a$, $b$ and $m$ are three numbers given above. We can express $x_n$ in terms of $\text{seed}$:
\[\begin{aligned} x_n &\equiv a x_{n-1} + b \equiv a \cdot (a x_{n-2} + b) + b \equiv a^2 \cdot x_{n-2} + b \cdot (a + 1) \\ &\equiv a^2 \cdot (a x_{n-3} + b) + b \cdot (a + 1) \equiv a^3 \cdot x_{n-3} + b \cdot (a^2 + a + 1) \\ &\equiv ... \equiv a^n \cdot x_0 + b \cdot (a^{n-1} + a^{n-2} + ... + 1) \\ &\equiv a^n \cdot \text{seed} + b \cdot (a^{n-1} + a^{n-2} + ... + 1) \quad (\text{mod}\ m) \end{aligned}\]
Interestingly, $m = 2^{64} \cdot 13337$ and $a$ and $b$ are multiple of 4 (that said, there exist integers $u$ and $v$ such that $a = 4u$ and $b = 4v$).
We can consider the whole thing under mod $2^{64}$:
\[\begin{aligned} x_n &\equiv a^n \cdot \text{seed} + b \cdot (a^{n-1} + a^{n-2} + ... + 1) \\ &\equiv (4u)^n \cdot \text{seed} + 4v \cdot [(4u)^{n-1} + (4u)^{n-2} + ... + 1] \quad (\text{mod}\ 2^{64}) \end{aligned}\]
In particular, when $n \geq 32$, we have $4^n = 2^{2n} = 2^{64} \cdot 2^{2n - 64} \equiv 0\ (\text{mod}\ 2^{64})$. We have:
\[\begin{aligned} x_n &\equiv (4u)^n \cdot \text{seed} + 4v \cdot [(4u)^{n-1} + (4u)^{n-2} + ... + 1] \\ &\equiv 4^n \cdot u^n \cdot \text{seed} + 4v \cdot [4^{n-1} \cdot u^{n-1} + 4^{n-2} \cdot u^{n-2} + ... + 1] \\ &\equiv 0 \cdot u^n \cdot \text{seed} + 4v \cdot [0 \cdot u^{n-1} + ... + 0 \cdot u^{32} + 4^{31} \cdot u^{31} + 4^{30} \cdot u^{30} + ... + 1] \\ &\equiv 4v \cdot [4^{31} \cdot u^{31} + 4^{30} \cdot u^{30} + ... + 1] \\ &\equiv 9640705563541584152 \quad (\text{mod}\ 2^{64}) \end{aligned}\]
This imply that $x_n\ \text{mod}\ 2^{64}$ is indepedent of the seed when $n$ is big. On the other hand, $x_n\ \text{mod}\ 13337$ is still unknown. Luckily there are only 13337 possibilities so we can exhaust them.
After all, for $n \geq 32$, there exists an integer $0 \leq u_n < 13337$ such that
\[x_n = 9640705563541584152 + 2^{64} \cdot u_n.\]
From here, we can devise with the below strategy:
- Play 34 rounds and obtain $x_{33}\ \text{mod}\ 12972$ and $x_{34}\ \text{mod}\ 12972$.
- Recover $x_{34}$ using $x_{33}\ \text{mod}\ 12972$ and $x_{34}\ \text{mod}\ 12972$.
- Compute $x_{35}, x_{36}, ..., x_{44}$ so that we can guess the words immediately.
- ??
- Profit!
If everything goes well, then we will obtain the flag:
MOCSCTF{c4n_y0u_pr3d1c7_th3_4ctu4l_w0rd13_s0lu71on5_n0w}By the way, it is much easier to get the answers for Wordle - they are hardcoded in the JavaScript files.
3-AES (Crypto, Misc)⌗
Challenge Summary⌗
Denote $\text{3AES}: \mathcal{M} \rightarrow \mathcal{C}$ by $c := \text{3AES}(m)$, where
\[\begin{aligned} t_1 &= \text{AES-CBC}_{k_1, \nu_1}(m) \\ t_2 &= \text{AES-CBC}_{k_2, \nu_2}(t_1) \\ c &= \text{AES-CBC}_{k_3, \nu_3}(t_2). \end{aligned}\]
When connected to the server, three sets of key-IV pairs $(k_i, \nu_i)$ (for $i = 1, 2, 3$) are generated. Here
key = md5(os.urandom(3)).digest()
iv = md5(os.urandom(6)).digest()We are allowed to call the below functions for an arbitrary number of times:
- [Encrypt message] Given $m$ and we get $\text{3AES}(m)$.
- [Encrypt flag] We get $\text{3AES}(\text{flag})$.
The objective is to recover the flag.
Solution⌗
The cipher does not behave as expected⌗
keys = [list()] * 3
def gen_keys():
for i in range(len(keys)):
key = md5(os.urandom(3)).digest()
iv = md5(os.urandom(6)).digest()
keys[i].append(key)
keys[i].append(iv)After gen_keys is called, one may expect keys would look like:
keys = [
[key1, iv1],
[key2, iv2],
[key3, iv3]
]This is indeed incorrect. In reality, keys would be:
keys = [
[key1, iv1, key2, iv2, key3, iv3],
[key1, iv1, key2, iv2, key3, iv3],
[key1, iv1, key2, iv2, key3, iv3]
]You can refer to this StackOverflow question for an explanation of the behaviour. Anyway, this is the actual definition of $\text{3AES}: \mathcal{M} \rightarrow \mathcal{C}$. Let $c := \text{3AES}(m)$, then
\[\begin{aligned} t_1 &= \text{AES-CBC}_{k, \nu}(m) \\ t_2 &= \text{AES-CBC}_{k, \nu}(t_1) \\ c &= \text{AES-CBC}_{k, \nu}(t_2). \end{aligned}\]
Here $k$ and $\nu$ are respectively key1 and iv1 defined above.
Attacking the cipher⌗
Since there are only $2^{24}$ possible keys, we can easily exhaust them to obtain $k$. If we have the right key, we can recover $\nu$ by sending 48 null bytes as the plaintext. In that way we have $m_1, m_2, m_3$ and $c_1, c_2, c_3$ as shown in the below figure. We omit the padding blocks ($m_4$ and $c_4$) for simplicity.
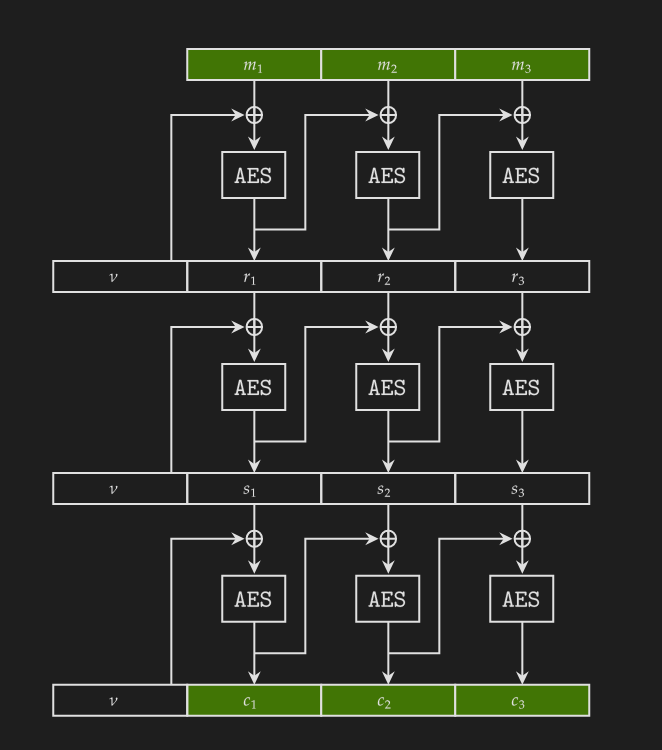
This is how we derive $\nu$ from $m_1, m_2, m_3$ and $c_1, c_2, c_3$ given a correct key ($\text{AESEnc}$ and $\text{AESDec}$ are respectively the encrypt and decrypt functions):
\[\begin{aligned} s_2 &:= c_1 \oplus \text{AESDec}_k(c_2) \\ s_3 &:= c_2 \oplus \text{AESDec}_k(c_3) \\ r_3 &:= s_2 \oplus \text{AESDec}_k(s_3) \\ r_2 &:= m_3 \oplus \text{AESDec}_k(r_3) \\ r_1 &:= m_2 \oplus \text{AESDec}_k(r_2) \\ \nu &:= m_1 \oplus \text{AESDec}_k(r_1) \end{aligned}\]
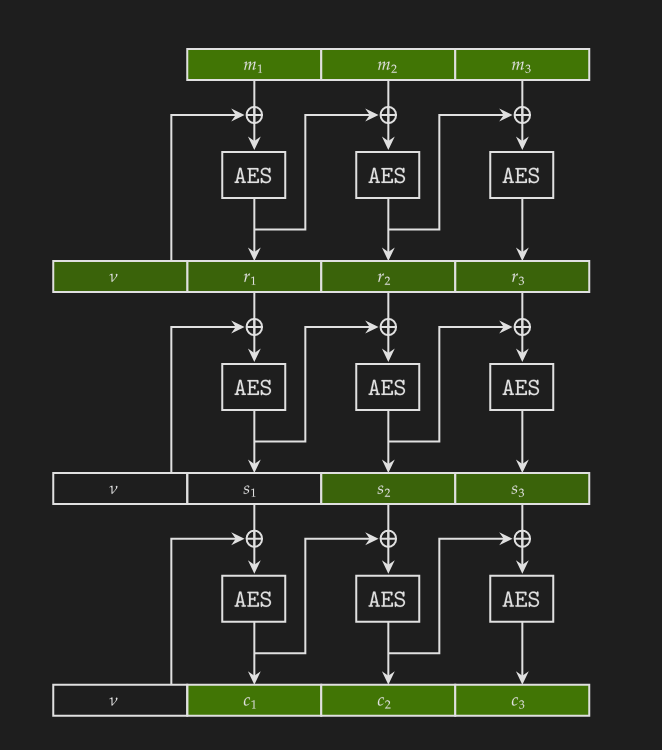
However, we do not know whether the key is correct. We can determine the correctness of the key by compute $c_1'$ and check if $c_1 = c_1'$:
\[\begin{aligned} s_1 &:= \text{AESEnc}(\nu \oplus r_1) \\ c_1' &:= \text{AESEnc}(\nu \oplus s_1) \end{aligned}\]
After we have the correct $(k, \nu)$, we can get $\text{3AES}(\text{flag})$ and decrypt:
MOCSCTF{pl34s3_h4nd13_y0ur_py7h0n_l1st5_w3ll}Elementary (Reverse)⌗
Challenge Summary⌗
- Download the program
- Execute the program.
- ??
- Profit!
Attachments: chall
We are given a Linux binary that prints the flag slowly. Players are expected to reverse the binary and optimize the algorithm.
Solution⌗
It is not difficult to see from decompilers (like IDA or Ghidra) that the program evaluates $\text{p}(0), \text{p}(1), ..., \text{p}(64)$ from a given polynomial $\text{p}$.
Why is it slow? This is how I define a + b, a * b and a ^ b (exponentation):
#define n 1000000007
// O(a + b)
int _add(int a, int b) {
int c = 0;
for (int i = 0; i < a; i++) c += 1;
for (int i = 0; i < b; i++) c += 1;
return c;
}
// O(a + b)
int _sub(int a, int b) {
int c = 0;
for (int i = 0; i < a; i++) c += 1;
for (int i = 0; i < b; i++) c -= 1;
return c;
}
// O(a + b)
int add(int a, int b) {
int c = _add(a, b);
if (c >= n) c = _sub(c, n);
return c;
}
// O(n * b)
int mul(int a, int b) {
int c = 0;
for (int i = 0; i < b; i++) {
c = add(c, a);
}
return c;
}
// O(n ^ b)
int pow(int a, int b) {
int c = 1;
for (int i = 0; i < b; i++) {
c = mul(c, a);
}
return c;
}Also, the coefficients of the polynomial is given in the main function:
int polynomial[] = {
77, 543680933, 779305823, 406010255, 852593453,
670940274, 400957584, 848777990, 534939184, 328847351,
616300066, 359055106, 161410101, 171509744, 155648929,
916365238, 18733844, 380452845, 509377978, 800691109,
908467961, 104753231, 181241660, 273070766, 93557074,
561221533, 449550761, 188262493, 915004277, 426375697,
665693795, 107906776, 665848870, 211169645, 53616008,
489964557, 908019215, 786707135, 573479073, 905263359,
938064888, 780724541, 361367421, 636367390, 816611492,
238098701, 596575814, 426971134, 943814120, 365926771,
929927764, 885597612, 895263918, 678662340, 387318491,
644785517, 566974198, 229009720, 874699826, 637234082,
673340960, 577186089, 903058253, 424604291, 663043221
};
// p(x) = 663043221 * x^55 + 424604291 * x^54 + ... + 543680933 * x + 77
Anyway it is easy to optimize the algorithm - you can just implement a + b, a * b and a ^ b in a standard way and the flag would be shown immediately:
MOCSCTF{th1s_pr0gr4m_1s_4lr34dy_sl0w_d01ng_ar1thm3t1c_0p3ra7i0n5}Redactor (Reverse)⌗
Challenge Summary⌗
I don't know, maybe you can run the program during the CTF and get a sense of what's going on.
Attachments: chall.exe
We are given a .exe file which is suggested to run in the background. Players may observe that the program would redact the flag (or part of the flag) that exists in the clipboard. For example, if one copies the first line from the clipboard, it became the second line after pasting.
MOCSCTF{what_is_this?}
********what_is_this?}Solution⌗
Since the program is compiled by PyInstaller, one may try PyInstaller Extractor to recover the source code (I did not try this, however).
If players are running the program during the CTF, I expect that they will be copy-pasting flags occasionally. The program redacts part of the flag they obtained and the players could have an insight on the behaviour of the program. We can obtain the flag byte-by-byte by exhausting the characters:
MOCSCTF{0 MOCSCTF{1 MOCSCTF{2 MOCSCTF{3 MOCSCTF{4 MOCSCTF{5 MOCSCTF{6 MOCSCTF{7
MOCSCTF{8 MOCSCTF{9 MOCSCTF{a MOCSCTF{b MOCSCTF{c MOCSCTF{d MOCSCTF{e MOCSCTF{f
MOCSCTF{g MOCSCTF{h MOCSCTF{i MOCSCTF{j MOCSCTF{k MOCSCTF{l MOCSCTF{m MOCSCTF{n
MOCSCTF{o MOCSCTF{p MOCSCTF{q MOCSCTF{r MOCSCTF{s MOCSCTF{t MOCSCTF{u MOCSCTF{v
MOCSCTF{w MOCSCTF{x MOCSCTF{y MOCSCTF{z MOCSCTF{A MOCSCTF{B MOCSCTF{C MOCSCTF{D
MOCSCTF{E MOCSCTF{F MOCSCTF{G MOCSCTF{H MOCSCTF{I MOCSCTF{J MOCSCTF{K MOCSCTF{L
MOCSCTF{M MOCSCTF{N MOCSCTF{O MOCSCTF{P MOCSCTF{Q MOCSCTF{R MOCSCTF{S MOCSCTF{T
MOCSCTF{U MOCSCTF{V MOCSCTF{W MOCSCTF{X MOCSCTF{Y MOCSCTF{Z MOCSCTF{! MOCSCTF{"
MOCSCTF{# MOCSCTF{$ MOCSCTF{% MOCSCTF{& MOCSCTF{' MOCSCTF{( MOCSCTF{) MOCSCTF{*
MOCSCTF{+ MOCSCTF{, MOCSCTF{- MOCSCTF{. MOCSCTF{/ MOCSCTF{: MOCSCTF{; MOCSCTF{<
MOCSCTF{= MOCSCTF{> MOCSCTF{? MOCSCTF{@ MOCSCTF{[ MOCSCTF{\ MOCSCTF{] MOCSCTF{^
MOCSCTF{_ MOCSCTF{` MOCSCTF{{ MOCSCTF{| MOCSCTF{} MOCSCTF{~It became the below after copy-pasting. Note that MOCSCTF{c has been replaced to ********* and therefore we know MOCSCTF{c is the prefix of the flag.
********0 ********1 ********2 ********3 ********4 ********5 ********6 ********7
********8 ********9 ********a ********b ********* ********d ********e ********f
********g ********h ********i ********j ********k ********l ********m ********n
********o ********p ********q ********r ********s ********t ********u ********v
********w ********x ********y ********z ********A ********B ********C ********D
********E ********F ********G ********H ********I ********J ********K ********L
********M ********N ********O ********P ********Q ********R ********S ********T
********U ********V ********W ********X ********Y ********Z ********! ********"
********# ********$ ********% ********& ********' ********( ********) *********
********+ ********, ********- ********. ********/ ********: ********; ********<
********= ********> ********? ********@ ********[ ********\ ********] ********^
********_ ********` ********{ ********| ********} ********~We can obtain the flag by repeating the process.
MOCSCTF{cryp70curr3ncy_4s537s_4r3_s0m3t1m3s_5tol3n_v1a_cl1pb04rd}- H. Krawczyk, M. Bellare, R. Canetti (1997) "HMAC: Keyed-Hashing for Message Authentication"
https://datatracker.ietf.org/doc/html/rfc2104#section-2 ↩