HACKING GOOGLE is a documentary of Google’s cybersecurity teams and H4CK1NG G00GL3 is it’s CTF counterpart. Project Zero Adventure is a cryptography challenge I wrote.

In the game, the players control the Security Princess to dodge the obstacles and catch the bugs (a variant of Google Chrome’s dinosaur game). After that, the server will sign messages consisting of the players' name and the score via the /sign API. The players will then submit it to the /highscore API. If the score submitted to the highscore API is negative, they will be given the flag.

However, there is one catch: The server is only willing to sign the results with non-negative scores.

Challenge Summary⌗

It is given that the server signs messages using a RSA key with a 2048-bit public modulus $n$ and $e = 3$. The messages are signed with PKCS#1 v1.5. The verify method below is how a signature s, correspond to the message m, is being verified. The goal is to forge a signature for messages indicating that the player has a negative score (one example of the message being ["pzero-adventures", "MYZ", -1]).

class VerifyingKey:
    def __init__(self, n, e, bits=2048):
        self.n = n
        self.e = e

        self.bits = bits

    # https://datatracker.ietf.org/doc/html/rfc2313#section-10.2
    # Note: The only hash algorithm we accept is SHA256.
    def verify(self, m, s):
        if len(s) != self.bits//8:
            raise Exception('incorrect signature length')
        s = int.from_bytes(s, 'big')

        k = pow(s, self.e, self.n)
        k = int.to_bytes(k, self.bits//8, 'big')
        if k[0] != 0x00:
            raise Exception('incorrect prefix')
        if k[1] != 0x01:
            raise Exception('incorrect prefix')
        
        padding, digest_info = k[2:].split(b'\x00', 1)

        if len(padding) < 8:
            raise Exception('invalid padding length')
        if padding != b'\xff'*len(padding):
            raise Exception('invalid padding content')

        sequence = DerSequence()
        sequence.decode(digest_info)
        _digest_algorithm_identifier, _digest = sequence

        sequence = DerSequence()
        sequence.decode(_digest_algorithm_identifier)
        _digest_algorithm_identifier = sequence[0]

        object_id = DerObjectId()
        object_id.decode(_digest_algorithm_identifier)
        digest_algorithm_identifier = object_id.value
        if digest_algorithm_identifier != '2.16.840.1.101.3.4.2.1':
            raise Exception('invalid digest algorithm identifier')

        _null = sequence[1]
        null = DerNull()
        null.decode(_null)

        octet_string = DerOctetString()
        octet_string.decode(_digest)
        digest = octet_string.payload

        if hashlib.sha256(m).digest() != digest:
            raise Exception('mismatch digest')
        return True

Solution⌗

📖 Alternative Writeups (which are usually better). Of course you would like to read the solutions from our players and our fellow Googlers! Writeup by @44670, writeup by @Dvd848, writeup by @dguerri and writeup by @paulsc.
⏩ Fast forward? If you are interested only in the solution, you can start reading from part III. I will begin with a literature review.

Part I: How PKCS#1 v1.5 signature scheme works?⌗

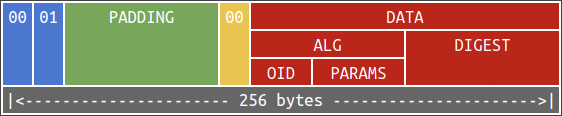
It is well-known that RSA sign messages by “decrypting” them. Assuming that the RSA key is of 256 bytes, the PKCS#1 v1.5 payload to be signed is given below:

Suppose that DATA is of length $l$. According to RFC 2313, PADDING consists of $253 - l$ bytes which are all 0xFF. Also, the data are encoded using Distinguished Encoding Rules (DER). Below is an example of DER-encoded data indicating that:

  • the hash algorithm being SHA-256, and
  • the digest being 0424974c68530290458c8d58674e2637f65abc127057957d7b3acbd24c208f93.
└─┬ 30 31                                  Sequence type (length 0x31)
  ├─┬ 30 0d                                Sequence type (length 0x0D)
  │ ├─┬ 06 09                              Object identifier type (length 0x09)
  │ │ └── 608648016503040201               Object identifier content (decoded
  │ │                                        2.16.840.1.101.3.4.2.1, SHA-256's OID)
  │ └── 05 00                              Null type (length 0x00)
  └─┬ 04 20                                Octet string type (length 0x20)
    └── 0424974c68530290458c8d58674e2637   Octet string content
        f65abc127057957d7b3acbd24c208f93

Let $m$ denote the PKCS#1 v1.5 payload. Then the signature is given by $s = m^d \ \text{mod}\ n$.

Part II: Bleichenbacher’s signature forgery attack in 2006⌗

In 2006, Bleichenbacher shared on CRYPTO'06 (Hal Finney’s summary) a way to easily forge RSA signatures when $e$ is small and the verify function is poorly implemented.

Suppose that the signature is validated by unpadding, retrieving ALGORITHM and DIGEST from DATA and discarding remaining bytes. This is an ideal message:

However, as long as the ALGORITHM and DIGEST are correct, messages in the below format are considered valid as well:

Yes – this is not properly validated. This is disastrous, why?

Let $e = 3$ and suppose we want to forge a signature for a message with its SHA-256 digest being 0424974c68530290458c8d58674e2637f65abc127057957d7b3acbd24c208f93.

Equivalently, we want to find $s$ with $s^3 \equiv m\ (\text{mod}\ n)$. Hereby $m$ begins with $m_0$ (which is 61 bytes long) below, i.e., $m = {256}^{195} m_0 + x$ for some “garbage” $x \in [0, {256}^{195})$.

m0 = 0x00 01 ffffffffffffffff 30 31 30 3d 06 09 608648016503040201 50 00 04 20 0424974c68530290458c8d58674e2637f65abc127057957d7b3acbd24c208f93
             [PADDING       ] [DATA                                                                                                           ]
                                    [ALGORITHM                         ] [DIGEST                                                              ]

It is difficult to work on modulo arithmetic, so let’s lift the modulo away and look for $s$ such that $s^3 = m = {256}^{165} m_0 + x$. It is easy to find a $s$ such that

$${256}^{165} m_0 \leq s^3 < {256}^{165} (m_0 + 1).$$

In short, any of the integer between $\sqrt[3]{{256}^{165} m_0}$ and $\sqrt[3]{{265}^{165} (m_0 + 1)}$ would fit – and that is basically Bleichenbacher’s attack in 2006.

Part III: …and it constantly strikes back⌗

It is still hard to validate PKCS#1 v1.5 signatures properly after a decade.

In 2016, Filippo Valsorda (@filosottile) wrote a blog post on a flaw on such message being validated. In short, it is the PADDING which is not properly validated. You can read the source code of the vulnerable function here.

This is not the end. In 2019, Sze Yiu Chau shared on Black Hat USA that the PKCS#1 v1.5 signatures are still not validated correctly (video and white paper here). This yields six CVEs to their research team from various TLS and IPSec libraries.

It is slightly different from BB'06. Instead of stuffing garbage as the suffix, we are putting random bytes in the middle. Mathematically, we are looking for $x$ with

$$s^3 = m = 256^{l_1} \cdot \text{prefix} + 256^{l_2} \cdot x + \text{suffix}$$

for a given $\text{prefix}$, $\text{suffix}$, $l_1$ and $l_2$.

This is harder than stuffing garbage at the very end, because we have to solve the below inequalities and congruences at the same time:

  • $256^{l_1} \cdot \text{prefix} \leq s^3 < 256^{l_1} \cdot (\text{prefix} + 1)$, and
  • $s^3 \equiv \text{suffix}\ (\text{mod}\ 256^{l_2}).$

Fortunately this is solvable when $l_1 - l_2$ is large (we can stuff more garbage in between) and $e$ is small. Let’s leave this as an exercise to the readers.

Part IV: …again in H4CK1NG G00GL3⌗

Now back to the challenge. The verify function at the very beginning seems to be implemented correctly. But there is one problem in the following snippet:

class VerifyingKey:
    # ...SKIPPED...

    def verify(self, m, s):
        # ...SKIPPED...

        sequence = DerSequence()
        sequence.decode(_digest_algorithm_identifier)
        _digest_algorithm_identifier = sequence[0]

        object_id = DerObjectId()
        object_id.decode(_digest_algorithm_identifier)
        digest_algorithm_identifier = object_id.value
        if digest_algorithm_identifier != '2.16.840.1.101.3.4.2.1':
            raise Exception('invalid digest algorithm identifier')

        _null = sequence[1]
        null = DerNull()
        null.decode(_null)

        octet_string = DerOctetString()
        octet_string.decode(_digest)
        digest = octet_string.payload

        if hashlib.sha256(m).digest() != digest:
            raise Exception('mismatch digest')
        return True

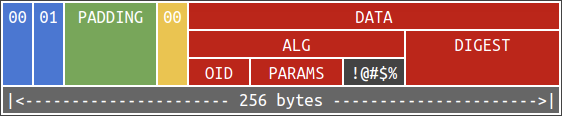
In the snippet, it checks if

  • the first item in the sequence is an object identifier being SHA-256’s OID, and
  • the second item in the sequence (i.e., the parameter) is a null object.

Unfortunately, the method did not check if the sequence has exactly two items. An adversary can insert garbage and pretend that being the third item in the sequence. We then can reduce this to the math problem mentioned in part III.

Part V: …and again, unexpectedly⌗

🤯 Unintended solution? I was carefully enough to make one mistake, but I was not carefully enough to make only one mistake. This part is dedicated to @XMPPwocky, who found an unintended solution and I was super surprised.

Finally, let’s patch the vulnerability. It is intuitive to check if the sequence of ALGORITHM has exactly two items:

class VerifyingKey:
    # ...SKIPPED...

    def verify(self, m, s):
        # ...SKIPPED...

        sequence = DerSequence()
        sequence.decode(digest_info)
        _digest_algorithm_identifier, _digest = sequence

        sequence = DerSequence()
        sequence.decode(_digest_algorithm_identifier)

+       if len(sequence) != 2:
+           raise Exception('invalid sequence length')

        _digest_algorithm_identifier = sequence[0]

        object_id = DerObjectId()
        object_id.decode(_digest_algorithm_identifier)
        digest_algorithm_identifier = object_id.value
        if digest_algorithm_identifier != '2.16.840.1.101.3.4.2.1':
            raise Exception('invalid digest algorithm identifier')

        _null = sequence[1]
        null = DerNull()
        null.decode(_null)

        octet_string = DerOctetString()
        octet_string.decode(_digest)
        digest = octet_string.payload

        if hashlib.sha256(m).digest() != digest:
            raise Exception('mismatch digest')
        return True

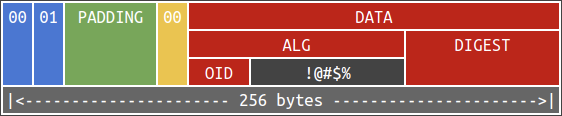
Is it sufficient? Surprisingly no. @XMPPwocky found a problem when decoding for DerNull – the latest version of pycryptodome (v3.15.0) does not raise an exception if it contains a non-empty payload!

Normally, a DerNull object consists of two bytes: 05 00. However, the below bytes are considered valid a DerNull object:

05 27 64696420796f75206c6f6f6b20757020666f7220746865206861736820696e207061727420493f

We can experiment this:

from Crypto.Util.asn1 import DerNull

_null = bytes.fromhex('05 27 64696420796f75206c6f6f6b20757020666f7220746865206861736820696e207061727420493f')
null = DerNull()
null.decode(_null) # This does not raise an exception!

With that said, we can actually stuff garbage in the parameter field. Once again it became the math puzzle in part III.

I tried my best to verify everything except the intended issue while implementing. The unintended solution is definitely a lesson for me. 🤩 VERY NICE CATCH! 🎉