HKCERT CTF 2022 Postmortem (II): Harder Crypto Challenges

We will continue walking through the remaining crypto challenges I wrote for HKCERT CTF 2022: Mystiz can't code, Slow keystream and King of Rock, Paper, Scissors.

亞洲協會香港中心 / Mystiz can't code (Crypto)⌗

Challenge Summary⌗

Mystiz can't code! He wanted to implement Advanced Encryption Standard (AES) in batch but he couldn't do it correctly.

Anyway, he decided to give up and uploads what he has for now. Since this is implemented based on AES, it should be almost as secure as AES as well?

Attachments: aes.bat, transcript.txt

We are given a batch script which attempts to implement AES. We are also given two ciphertexts encrypted with the same key (and one of the plaintexts is given).

Microsoft Windows [Version 10.0.19044.2006]
(c) Microsoft Corporation. All rights reserved.

C:\Users\mystiz>aes.bat [**REDACTED_KEY**] 68656c6c6f20776f726c6421
2740f489df8449453fd87f075a648e94

C:\Users\mystiz>aes.bat [**REDACTED_KEY**] [**REDACTED_FLAG**]
9a3538b25faf70f2654e7816df540acedb753d319f76311d95a4ad5e797fff3e13f7dcbde563baf8f7ac62580196b5ca911789fedade0fd6fb40642413d521992311f9bc01d127db4bbcf257ee5deb8fcd49b23aadd12f52fa7829e7e281373f

Solution⌗

Part I: Background story⌗

I am a newbie to batch scripts. The only batch script I wrote was to shut down a machine. Back in the day MSN still exists (an application in the stone age, huh?), I used to rename those batch scripts into files, changed their icons and sent them to my friends. It was pretty satisfying when you see they became offline as soon as they receive the files.

Well, after uncountably many years, I am asked to write batch scripts for my work to maintain Windows machines. I was stuck into an issue for a few hours... and it was pretty amusing. Anyway, I thought that is worth making it into a CTF challenge.

Part II: Understanding the cipher⌗

Denote the flawed AES by $\text{AES}^\dagger$. When we compare the batch script with the below figure showing the implementation, it seems that everything matches.

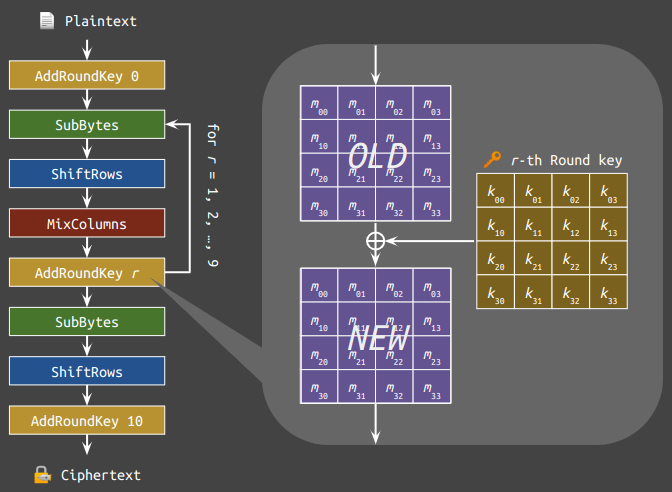
For instance, the EncryptBlock and the AddRoundKey functions below looked legit (except that the state is a global variable).

:EncryptBlock
    set block_id=%1

    call :LoadState %block_id%

    set round_key=0
    call :AddRoundKey %round_key%

    for /l %%r in (1, 1, 9) do (
        set round_key=%%r
        call :SubBytes
        call :ShiftRows
        call :MixColumns
        call :AddRoundKey %round_key%
    )

    set round_key=10
    call :SubBytes
    call :ShiftRows
    call :AddRoundKey %round_key%
    
    call :SaveState %block_id%
exit /b 0

:AddRoundKey
    set round_id=%1
    for /l %%i in (0, 1, 15) do (
        set /a j=16*%round_id%+%%i
        set /a STATE[%%i]="STATE[%%i]^KEY[%j%]"
    )
exit /b 0

If you are convinced, then unfortunately you fell into the same pitfall as I did. In reality, there is a bizarre behaviour that I couldn't understand while writing the challenge. In short, both EncryptBlock and AddRoundKey are flawed so that $\text{AES}^\dagger$ is not working as intended. The below figure shows how the messages are encrypted using $\text{AES}^\dagger$. $n$ in the figure is the number of blocks the script has encrypted.

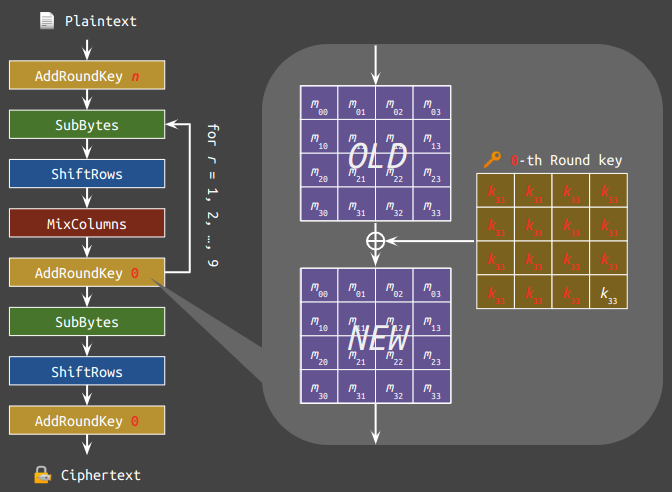
We can see from above that only two bytes from the subkeys are used when encrypting a block, which is $k_{33}$ from the 0-th and the $n$-th round keys. The other parts are performed in the same way that AES does. Up to here, we can already write a script to exhaust the $2^{16}$ subkey candidates for each block.

hkcert22{pr09r4mm1ng_in_b47ch_1s_s0_d1fficul7_4nd_why_d03s_th1n9s_1n_br4ck3t_run5_in_p4ral13l}

Part III: Batch, why?⌗

In this section, we will study the causes of the problem. In short, the commands in the parentheses are executed simultaneously¹.

For batch scripts, all function variables are global unless we specify SETLOCAL in the function. Let's consider how the first block is encrypted. It calls LoadState at the very beginning, which eventually sets $j \leftarrow 15$. Since $j$ is global, its value will be shared. After that, AddRoundKey, which is defined below, is called with the argument round_id = 0.

:AddRoundKey
    set round_id=%1
    for /l %%i in (0, 1, 15) do (
        set /a j=16*%round_id%+%%i
        set /a STATE[%%i]="STATE[%%i]^KEY[%j%]"
    )
exit /b 0

Since the commands are executed simultaneously, $j$ was unable to update timely when it is used to update the state. The value of $j$ in the line that sets the value of STATE[i] is fixed for all $i = 0, 1, ..., 15$. Therefore, instead of XORing the message with the round key, every byte of the message is XORed with KEY[15] (i.e., $k_{33}$ from the 0-th round key).

:EncryptBlock
    set block_id=%1

    call :LoadState %block_id%

    set round_key=0
    call :AddRoundKey %round_key%

    for /l %%r in (1, 1, 9) do (
        set round_key=%%r
        call :SubBytes
        call :ShiftRows
        call :MixColumns
        call :AddRoundKey %round_key%
    )

    set round_key=10
    call :SubBytes
    call :ShiftRows
    call :AddRoundKey %round_key%
    
    call :SaveState %block_id%
exit /b 0

Let's have a look at the EncryptBlock function. The parameter for the AddRoundKey function, %round_key%, is actually zero for all the rounds. This sets $j \leftarrow 15$ when AddRoundKey is called, which will be used in the final AddRoundKey call. With that said, when $n = 0$, only KEY[15] will be used for encryption.

On the other hand for $n > 0$, LoadState sets $j \leftarrow 16n+15$. This $j$ will only be used on the first AddRoundKey (and the subsequent $j$s for AddRoundKey are 15), which implies that KEY[16*n+15] (i.e., $k_{33}$ of the $n$-th round key) will be used for the first AddRoundKey and $k_{33}$ of the 0-th round key.

澳洲牛奶公司 / Slow keystream (Crypto)⌗

Challenge Summary⌗

Want a challenge in Hong Kong?

Enter the Australia Dairy Company and execute the 379-byte flag generator written in Golang. I bet you will be expelled from the restaurant before the second character of the flag appears.

Attachments: flag, flag.enc, flag.go

We are given a binary written in Golang (with source code given below), and flag.enc. The objective is to recover the input.

package main

import (
	"fmt"
	"math/rand"
	"os"
)

func main() {
	rand.Seed(1337)

	flag, err := os.ReadFile("flag.enc")
	if err != nil {
		fmt.Println("cannot open flag.enc")
		os.Exit(1)
	}

	for i, j := uint64(0), 0; j < len(flag); i++ {
		rand.Uint64()
		if i == uint64(1)<<j {
			x := byte(rand.Uint64())
			fmt.Print(string(flag[j] ^ x))
			j += 1
		}
	}
	fmt.Println()
}

Solution⌗

Part I: What is in Golang's PRNG?⌗

In this challenge, the characters of the encrypted flag is XORed with the outputs from rand.Uint64. With that said, we have to look deeper into the internals of the PRNG. We can start with the documentation - with that, we can read the source code and see where the actual code is. Tracing in the codebase, eventually, we end up at its implementation (snippets below):

// https://cs.opensource.google/go/go/+/refs/tags/go1.19:src/math/rand/rng.go

// Copyright 2009 The Go Authors. All rights reserved.
// Use of this source code is governed by a BSD-style
// license that can be found in the LICENSE file.

package rand

/*
 * Uniform distribution
 *
 * algorithm by
 * DP Mitchell and JA Reeds
 */

const (
	rngLen   = 607
	rngTap   = 273
	rngMax   = 1 << 63
	rngMask  = rngMax - 1
	int32max = (1 << 31) - 1
)

var (
	// rngCooked used for seeding. See gen_cooked.go for details.
	rngCooked [rngLen]int64 = [...]int64{
		-4181792142133755926, -4576982950128230565, 1395769623340756751, 5333664234075297259,
		// ...600 numbers snipped...
		8382142935188824023, 9103922860780351547, 4152330101494654406,
	}
)

type rngSource struct {
	tap  int           // index into vec
	feed int           // index into vec
	vec  [rngLen]int64 // current feedback register
}

// seed rng x[n+1] = 48271 * x[n] mod (2**31 - 1)
func seedrand(x int32) int32 {
	const (
		A = 48271
		Q = 44488
		R = 3399
	)

	hi := x / Q
	lo := x % Q
	x = A*lo - R*hi
	if x < 0 {
		x += int32max
	}
	return x
}

// Seed uses the provided seed value to initialize the generator to a deterministic state.
func (rng *rngSource) Seed(seed int64) {
	rng.tap = 0
	rng.feed = rngLen - rngTap

	seed = seed % int32max
	if seed < 0 {
		seed += int32max
	}
	if seed == 0 {
		seed = 89482311
	}

	x := int32(seed)
	for i := -20; i < rngLen; i++ {
		x = seedrand(x)
		if i >= 0 {
			var u int64
			u = int64(x) << 40
			x = seedrand(x)
			u ^= int64(x) << 20
			x = seedrand(x)
			u ^= int64(x)
			u ^= rngCooked[i]
			rng.vec[i] = u
		}
	}
}

// Uint64 returns a non-negative pseudo-random 64-bit integer as an uint64.
func (rng *rngSource) Uint64() uint64 {
	rng.tap--
	if rng.tap < 0 {
		rng.tap += rngLen
	}

	rng.feed--
	if rng.feed < 0 {
		rng.feed += rngLen
	}

	x := rng.vec[rng.feed] + rng.vec[rng.tap]
	rng.vec[rng.feed] = x
	return uint64(x)
}

Part II: Fibonnnnacccci and its matrix representation⌗

We can see that rng.vec is an array of 607 64-bit numbers. When Uint64 is called, two numbers from the array are retrieved, summed and returned. The sum will be stored in the array for future calls. Let $v^{(n)} := (v_0^{(n)}, v_1^{(n)}, ..., v_{606}^{(n)})$ be the vector after $n$ Uint64 calls. Then the first two $v^{(n)}$s being:

\[v^{(1)}_k := \begin{cases} v^{(0)}_{333} + v^{(0)}_{606} & \text{if}\ k = 333 \\ v^{(0)}_k & \text{otherwise} \end{cases}, \qquad v^{(2)}_k := \begin{cases} v^{(1)}_{332} + v^{(1)}_{605} & \text{if}\ k = 332 \\ v^{(1)}_k & \text{otherwise} \end{cases}, ...\]

It is obvious that Uint64 changes only one entry at a time. Let's define

\[(a_0, a_1, ..., a_{606}) := (v^{(0)}_{333}, v^{(0)}_{332}, ..., v^{(0)}_{0}, v^{(0)}_{606}, v^{(0)}_{605}, ..., v^{(0)}_{334}).\]

Furthermore, let also $a_{607}, a_{608}, ...$ be the only changing entry in each round, i.e., $a_{607} := v^{(1)}_{333}$, $a_{608} := v^{(2)}_{332}$ and so on. Therefore $a_{607} = a_0 + a_{334}, a_{608} = a_1 + a_{335}, ...$.

This is simply a lagged Fibonacci generator. We can represent it as a matrix multiplication, which will be useful when we compute the values efficiently:

\[\begin{bmatrix}a_{k+1} \\ a_{k+2} \\ a_{k+3} \\ \vdots \\ a_{k+335} \\ \vdots \\ a_{k+606} \\ a_{k+607} \end{bmatrix} = \left[\begin{array}{c|ccccccc} 0 && 1 && 0 && ... && && ... && 0 && 0 \\ 0 && 0 && 1 && ... && && ... && 0 && 0 \\ \ && && && && && && && \\ \vdots && && && && \ddots && && && \\ \ && && && && && && && \\ 0 && 0 && 0 && ... && && ... && 0 && 1 \\ \hline 1 && 0 && 0 && ... && 1 && ... && 0 && 0 \end{array}\right] \begin{bmatrix}a_k \\ a_{k+1} \\ a_{k+2} \\ \vdots \\ a_{k+334} \\ \vdots \\ a_{k+605} \\ a_{k+606} \end{bmatrix}\ (\text{mod}\ 2^{64}).\]

If we let $T$ be the huge square matrix, then for all $n \in \mathbb{Z}_{\geq 0}$, we have

\[\begin{bmatrix}a_{n} \\ a_{n+1} \\ \vdots \\ a_{n+606}\end{bmatrix} = T \begin{bmatrix}a_{n-1} \\ a_{n} \\ \vdots \\ a_{n+605}\end{bmatrix} = T^2 \begin{bmatrix}a_{n-2} \\ a_{n-1} \\ \vdots \\ a_{n+604}\end{bmatrix} = ... = T^n \begin{bmatrix}a_0 \\ a_1 \\ \vdots \\ a_{606} \end{bmatrix}(\text{mod}\ 2^{64}).\]

Part III: The final steps⌗

Finally, let's revisit flag.go:

func main() {
	rand.Seed(1337)

	flag, err := os.ReadFile("flag.enc")
	if err != nil {
		fmt.Println("cannot open flag.enc")
		os.Exit(1)
	}

	for i, j := uint64(0), 0; j < len(flag); i++ {
		rand.Uint64()
		if i == uint64(1)<<j {
			x := byte(rand.Uint64())
			fmt.Print(string(flag[j] ^ x))
			j += 1
		}
	}
	fmt.Println()
}

Let $n$ be the length of the flag. The below flow explains which rand.Uint64() are used after the random is seeded:

1. Generate two unused rand.Uint64() and set $k \leftarrow 0$.
2. Generate a rand.Uint64() to decrypt the $k$-th byte from flag.enc.
3. Generate $2^{k+1}$ unused rand.Uint64().
4. If $k < n-1$, set $k \leftarrow k + 1$ and jump to step 2. Otherwise, we are done.

Equivalently, this is the draft of the solve script:

1. Initialize $M$ be the $607 \times 607$ matrix, set $\bold{a} \leftarrow (a_0, a_1, ..., a_{607})$ and $k \leftarrow 0$.
2. Set $\bold{a} \leftarrow M^2 \cdot \bold{a}$.
3. Set $\bold{a} \leftarrow T \cdot \bold{a}$.
4. Decrypt the $k$-th character of the flag from the last entry of $\bold{a}$.
5. Set $\bold{a} \leftarrow S \cdot \bold{a}$ and $S \leftarrow S^2$.
6. If $k < n-1$, set $k \leftarrow k + 1$ and jump to step 3. Otherwise, we are done.

In particular, step 5 is used for "fast forwarding". If $S = T^m$, then $\bold{a} \leftarrow S \cdot \bold{a}$ is a way to skip $m$ steps at a time. Also, $S \leftarrow S^2$ sets $S$ to $T^{2m}$, which makes subsequent calls to skip $2m$ steps.

Solve script⌗

RNGCOOKED = [
    -4181792142133755926, -4576982950128230565, 1395769623340756751, 5333664234075297259,
    # ...Snipped. Please copy directly from Golang's source code 
    8382142935188824023, 9103922860780351547, 4152330101494654406
]
RNGLEN = 607
RNGTAP = 273

class GoRng:
    def __init__(self, seed):
        self.tap = 0
        self.feed = RNGLEN - RNGTAP

        self.vec = vector(Zmod(2^8), [0 for _ in range(RNGLEN)])

        seed %= (1<<31) - 1
        if seed == 0: seed = 89482311

        x = seed
        for i in range(-20, 0):
            x = self.__seedrand(x)

        for i in range(RNGLEN):
            x = self.__seedrand(x)
            u = x<<40
            x = self.__seedrand(x)
            u ^^= x<<20
            x = self.__seedrand(x)
            u ^^= x
            u ^^= RNGCOOKED[i]
            self.vec[i] = u

    def __seedrand(self, x):
        A, Q, R = 48271, 44488, 3399
        hi = x // Q
        lo = x % Q
        x = A*lo - R*hi
        return x % ((1<<31) - 1)


rng = GoRng(1337)

T = Matrix(Zmod(2^8), 607, 607)

for i in range(606):
    T[i, i+1] = 1
T[606, 0]     = 1
T[606, 334]   = 1

S = T

a = vector(Zmod(2^8), list(rng.vec[333::-1]) + list(rng.vec[:333:-1]))

# Skip the first two randoms
a = T^2 * a

with open('flag.enc', 'rb') as f: flag = f.read()
output = []
for i, f in enumerate(flag):
    a = T*a
    output.append(int(a[-1]) ^^ f)
    a = S*a
    S = S*S
    print(bytes(output))

海帆道 / King of Rock, Paper, Scissors (Crypto)⌗

Challenge Summary⌗

Let's play rock paper scissors securely. Since we are using a commitment scheme, none of us can cheat!

nc HOST PORT

Attachments: chall.py, client.py, game.proto, game_pb2.py

In this challenge, all messages are transmitted via protocol buffers (protobuf). Messages related to the protocol are given below:

message ServerRoundInitMessage {
  bytes nonce = 1; // server's nonce
}

message ClientRoundInitMessage {
  bytes hash = 1;  // MD5 digest of ClientMoveMessage
  bytes nonce = 2; // client's nonce
}

message ServerMoveMessage {
  Move move = 1;
}

message ClientMoveMessage {
  bytes nonce_server = 1;
  bytes nonce_client = 2;
  Move move = 3;
}

message ServerRoundFinalMessage {
  Player winner = 1;
};

Define a commitment scheme $\mathcal{C}$ between two parties (the server and the client) to play rock paper scissors, define the protocol below:

1. The server generates a nonce and sends the ServerRoundInitMessage to the client.
2. The client
   • determines a move (rock, scissors or stone),
   • generates a nonce,
   • constructs a ClientMoveMessage and computes its MD5 digest,
   • constructs a ClientRoundInitMessage, and
   • sends the ClientRoundInitMessage to the server.
3. The server determines a move and sends the ServerMoveMessage to the client.
4. The client sends the ClientMoveMessage to the server.
5. The server sends the ServerRoundFinalMessage to the client on who's the winner.

A game consists of 128 rounds. The objective is to win more than 95% of the rounds and lose none of them.

Solution⌗

Part I: A short demo of the protocol⌗

Step 1: ServerRoundInitMessage (Server → Client)⌗

Initially, the server generates a nonce 15f0...5273, constructs and sends the below ServerRoundInitMessage to the client.

// ServerRoundInitMessage
{"nonce": "15f0...5273"}

Step 2: ClientRoundInitMessage (Client → Server)⌗

The client wants to play scissors this time. It generates a nonce d7b5...1ff1. The client constructs a ClientMoveMessage message and its MD5 digest is 03e0...a148.

// ClientMoveMessage
{"nonce_server": "15f0...5273", "nonce_client": "d7b5...1ff1", "move": "scissors"}

Afterwards, the client constructs ClientRoundInitMessage with the client's nonce and the hash, and sends it to the server:

// ClientRoundInitMessage
{"hash": "03e0...a148", "nonce": "d7b5...1ff1"}

Step 3: ServerMoveMessage (Server → Client)⌗

At this stage, the server does not know what the client's move is. The server wants to play rock. It constructs the ServerMoveMessage and sends it to the player:

// ServerMoveMessage
{"move": "rock"}

Step 4: ClientMoveMessage (Client → Server)⌗

The client reveals the commitment by sending the ClientMoveMessage to the server (which is already constructed in step 2).

// ClientMoveMessage
{"nonce_server": "15f0...5273", "nonce_client": "d7b5...1ff1", "move": "scissors"}

Step 5: ServerRoundFinalMessage (Server → Client)⌗

The server can verify the validity of ClientMoveMessage, by checking whether

1. [client nonce] its client nonce equals the nonce in ClientRoundInitMessage,
2. [server nonce] its server nonce equals the nonce in ServerRoundInitMessage, and
3. [digest] its MD5 digest equals the hash specified in ClientRoundInitMessage.

Since everything checks out, the message is valid. The server finally knows that the client played scissors. Since the server plays rock, it wins the round. The server also sends a ServerRoundFinalMessage announcing their win:

// ServerRoundFinalMessage
{"winner": "server"}

Part II: Attacks related to MD5⌗

MD5 is insecure. It is very easy to find an MD5 collision in 2022. corkami/collisions is a repository explaining all sorts of hash collisions. There are various attacks, FastColl, UniColl and HashClash, and each of them has a different running speed and capability.

In short, we can forge a move without changing the MD5 digest. An idea would be to inject some "junk" fields that no one cared. They are not used to validate anything while affecting the hashed outcome.

To achieve this, we will use UniColl. Given a payload $p$ of length $64n+4k$ (for some small $k$'s), it will generate a pair of outputs $m_1$ and $m_2$ such that

1. The lengths of $m_1$ and $m_2$ are $64n+128$ bytes,
2. $\text{MD5}(m_1) = \text{MD5}(m_2)$,
3. $m_1$ begins with $p$, and
4. Only two bytes of $m_1$ and $m_2$ are different, which are the $(64n+10)$-th byte and the $(64n+74)$-th byte (one-indexed). Also, $m_1[64n+10] - m_2[64n+10] = 1$ and $m_1[64n+74] - m_2[64n+74] = -1$.

This is an example of a MD5 collision that UniColl finds. Suppose I want to find a pair of colliding messages starting with hello world. (and the other starts with hello wormd!, which is also 12 bytes long). We will use HashClash as a demo.

# Inside hashclash/scripts/demo
echo -n "hello world." > prefix.txt
../poc_no.sh prefix.txt
MD5 differential path toolbox
Copyright (C) 2009 Marc Stevens
http://homepages.cwi.nl/~stevens/
(trimmed)
Found collision!
468115c46b73eac261b6d9f5284b68e3  collision1.bin
468115c46b73eac261b6d9f5284b68e3  collision2.bin
31dda9646624a15c6078582c9af60cf597949a18  collision1.bin
87fbd7c43d1ed226d13a478f0b89f55a744864d9  collision2.bin
4 -rw-rw-r-- 1 mystiz mystiz 128 Dec 18 14:48 collision1.bin
4 -rw-rw-r-- 1 mystiz mystiz 128 Dec 18 14:48 collision2.bin
hd collision1.bin            
00000000  68 65 6c 6c 6f 20 77 6f  72 6c 64 2e 12 d9 a6 74  |hello world....t|
00000010  d7 a8 55 aa c5 66 63 f8  58 98 89 71 e8 b2 49 52  |..U..fc.X..q..IR|
00000020  f9 e0 de f1 a0 62 e4 0d  ba a9 57 b1 96 ed 91 eb  |.....b....W.....|
00000030  1c b7 69 1d 36 89 e7 1a  a2 41 a4 fd 7f bb 98 1f  |..i.6....A......|
00000040  f7 72 24 73 6b 78 6b 20  14 db d0 a2 36 66 2a bc  |.r$skxk ....6f*.|
00000050  36 fe cb 1e 32 1b 35 5b  b7 ce d7 1b 0f e5 3f 98  |6...2.5[......?.|
00000060  1b 8b ed ab 73 14 fb f7  57 d2 2d ed c9 45 8a 1c  |....s...W.-..E..|
00000070  2c f0 ab 4e fb 47 96 81  75 4c 25 34 ad ec 01 db  |,..N.G..uL%4....|
00000080
hd collision2.bin
00000000  68 65 6c 6c 6f 20 77 6f  72 6d 64 2e 12 d9 a6 74  |hello wormd....t|
00000010  d7 a8 55 aa c5 66 63 f8  58 98 89 71 e8 b2 49 52  |..U..fc.X..q..IR|
00000020  f9 e0 de f1 a0 62 e4 0d  ba a9 57 b1 96 ed 91 eb  |.....b....W.....|
00000030  1c b7 69 1d 36 89 e7 1a  a2 41 a4 fd 7f bb 98 1f  |..i.6....A......|
00000040  f7 72 24 73 6b 78 6b 20  14 da d0 a2 36 66 2a bc  |.r$skxk ....6f*.|
00000050  36 fe cb 1e 32 1b 35 5b  b7 ce d7 1b 0f e5 3f 98  |6...2.5[......?.|
00000060  1b 8b ed ab 73 14 fb f7  57 d2 2d ed c9 45 8a 1c  |....s...W.-..E..|
00000070  2c f0 ab 4e fb 47 96 81  75 4c 25 34 ad ec 01 db  |,..N.G..uL%4....|
00000080
md5sum collision*.bin
468115c46b73eac261b6d9f5284b68e3  collision1.bin
468115c46b73eac261b6d9f5284b68e3  collision2.bin

We can see the properties we mentioned - $m_1$ and $m_2$ have the same digest, and $m_1$ and $m_2$ differs by two bytes. Before we solve the challenge with UniColl, let's look at the protobuf message format.

Part III: Walk-through on protobuf message format⌗

A protobuf message consists of a series of records, which is composed of three items: the field number, the wire type and the content. Let's look at the wire type first.

The wire types⌗

We will only mention two wire types: VARINT and LEN because they are the only types that are used in ClientMoveMessage. It is probably not what you expect -- we used bytes and Move (which is an enum) instead of those types!

In reality, VARINT is a wire type that is used when transmitting the data types int32, int64, enum and so on. It uses a $k$-byte buffer to represent an unsigned integer not longer than $7k$-bit long. A one-byte VARINT can express up to $127$, and a two-byte VARINT can express up to $16383 = 2^{14} - 1$. Also, the most significant bit from each byte is considered to be the "continuation bit", which determines whether the subsequent byte belongs to the VARINT.

Below is an example of a VARINT of three bytes long (represented as binary):

[byte 1] [byte 2] [byte 3]
11000000 10100000 00010000
*(   64) *(   32)  (   16)

We can see that the MSB of the first two bytes are 1 and the MSB of the last byte is 0. This happens on every VARINT: All MSBs are 1 except the last byte. After that, we will interpret the integer from its base 128 expressions:

\[64 \cdot 128^0 + 32 \cdot 128^1 + 16 \cdot 128^2 = 266304.\]

Now two exercises.

For exercise 1, only the first entry is a valid VARINT. The answer for exercise 2 is $1337 = 0001010\ 0111001_2$.

Now onto the wire type LEN. One data type it can handle is bytes. Its expression is straightforward -- it begins with a VARINT consisting of the length $l$, followed by $l$ bytes being the buffer. For example, the below LEN is equivalent to hello:

00000101 01101000 01100101 01101100 01101100 01101111
********                                              -- an unsigned integer 5
         ******** ******** ******** ******** ******** -- 5-byte buffer "hello" 

There are two more types, I64 and I32, which are self-explanatory and I will not cover them. Each of the four wire types is assigned with a type ID:

Formation of messages⌗

Recall that a record is composed of a field number, a wire type and the content. We described the latter two since they are related. What about the field number?

enum Move {
  ROCK = 0;
  PAPER = 1;
  SCISSORS = 2;
}

message ClientMoveMessage {
  bytes nonce_server = 1;
  bytes nonce_client = 2;
  Move move = 3;
}

From the ClientMoveMessage above, the field numbers of nonce_server, nonce_client and move are 1, 2 and 3 respectively.

Now we understand everything and can finally build a field. A field begins with a VARINT given by $8f+t$ ($f$ and $t$ are the field number and the wire type), followed by the content. The 7-byte field below represents nonce_server to hello.

0a 05 68 65 6c 6c 6f
**                   -- an unsigned integer 10 = 8*1 + 2
                          field number = 1 (nonce_server)
                          wire type = 2 (LEN)
   **                -- an unsigned integer 5 (the length)
      ** ** ** ** ** -- 5-byte buffer "hello" 

Finally, a message is just a concatenation of records. Let's use ClientMoveMessage as an example:

The three red bytes $\text{0A}_{16} = 8 \cdot 1 + 2$, $\text{12}_{16} = 8 \cdot 2 + 2$ and $\text{18}_{16} = 8 \cdot 3 + 0$ respectively represent a LEN with field number 1 (nonce_server), a LEN with field number 2 (nonce_client) and a VARINT with field number 3 (move).

nonce_server: 1a0ab7c21d1c0200ffe48b8e0e37d369 (hex-encoded)
nonce_client: 152b631ddef3cd401dc0b730739460a8 (hex-encoded)
move: SCISSORS

There are quite some details that I did not cover yet. Since this subsection is overly long, I will talk about it when we need them.

Part IV: Generating the first pair of collision⌗

Now the goal is clear: For any nonce_server, find three ClientMoveMessages such that their nonce_clients are all the same, their moves are all different and the MD5 digests are the same. Here is the first property on protobuf:

For instance, type wire type I64 does not handle enums. Thus the below record is omitted when parsing ClientMoveMessage.

19 01 0a 05 04 05 06 07 08
**                         -- an unsigned integer 0x19 = 8*3 + 1
                                field number = 3 (move)
                                wire type = 1 (I64)
   ** ** ** ** ** ** ** ** -- the 64-bit integer 0x0807060504050a01

Besides, if we change the first byte to 18, it breaks down into two valid records:

18 01 0a 05 04 05 06 07 08
**                         -- an unsigned integer 0x18 = 8*3 + 0
                                field number = 3 (move)
                                wire type = 0 (VARINT)
   **                      -- an unsigned integer 1
      **                   -- an unsigned integer 0x0a = 8*1 + 2
                                field number = 1 (nonce_server)
                                wire type = 2 (LEN)
         **                -- an unsigned integer 5 (the length)
            ** ** ** ** ** -- 5-byte buffer "04 05 06 07 08"

nonce_server: 0405060708 (hex-encoded)
move: PAPER

Let's make a pair of ClientMoveMessages with the same MD5 digest and the moves being ROCK and PAPER, and will tackle SCISSORS later. Also, since nonce_server and nonce_client can be handled easily, we will not deal with them now.

This is a 20-byte prefix I made for Unicoll and it is expected that the size of the outputs is 128 bytes long.

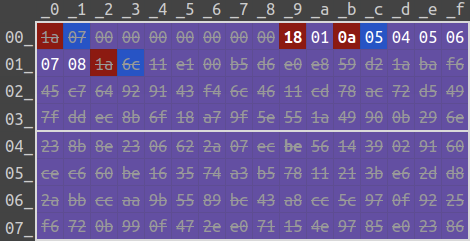
1a 07 00 00 00 00 00 00 00 18 01 0a 05 04 05 06 07 08 1a 6c

These are the outputs from Unicoll:

1a 07 00 00 00 00 00 00 00 18 01 0a 05 04 05 06 07 08 1a 6c 11 e1 00 b5 d6 e0 e8 59 d2 1a ba f6
45 c7 64 92 91 43 f4 6c 46 11 cd 78 ac 72 d5 49 7f dd ec 8b 6f 18 a7 9f 5e 55 1a 49 90 0b 29 6e
23 8b 8e 23 06 62 2a 07 ec be 56 14 39 02 91 60 ce c6 60 be 16 35 74 a3 b5 78 11 21 3b e6 2d d8
2a bb cc aa 9b 55 89 bc 43 a8 cc 5c 97 0f 92 25 f6 72 0b 99 0f 47 2e e0 71 15 4e 97 85 e0 23 86

1a 07 00 00 00 00 00 00 00 19 01 0a 05 04 05 06 07 08 1a 6c 11 e1 00 b5 d6 e0 e8 59 d2 1a ba f6
45 c7 64 92 91 43 f4 6c 46 11 cd 78 ac 72 d5 49 7f dd ec 8b 6f 18 a7 9f 5e 55 1a 49 90 0b 29 6e
23 8b 8e 23 06 62 2a 07 ec bd 56 14 39 02 91 60 ce c6 60 be 16 35 74 a3 b5 78 11 21 3b e6 2d d8
2a bb cc aa 9b 55 89 bc 43 a8 cc 5c 97 0f 92 25 f6 72 0b 99 0f 47 2e e0 71 15 4e 97 85 e0 23 86 

Both of the messages have MD5 digest 9c456db27e76b061617914bcb8d20f74. Now let's introduce one more property before we illustrate them.

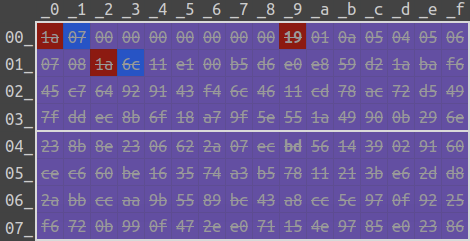
The first message composes of four records:

move = bytes.fromhex('00 00 00 00 00 00 00')   # bytes
move = 1                                       # enum, equivalent to "PAPER"
nonce_client = bytes.fromhex('04 05 06 07 08') # bytes
move = bytes.fromhex('11 e1 00 ... e0 23 86')  # bytes

Since it is illegal to assign move as bytes (it is an enum), only the second and the third records will be kept. Therefore, only two fields are assigned.

nonce_server: 0405060708 (hex-encoded)
move: PAPER

Besides, the second message composes of three records but none of them is valid. Since no moves are assigned, it uses the default value, ROCK.

move = bytes.fromhex('00 00 00 00 00 00 00')   # bytes
move = 0x08_07_06_05_04_05_0a_01               # fixed64
move = bytes.fromhex('11 e1 00 ... e0 23 86')  # bytes

Part V: Let's collide with scissors, too⌗

MD5 uses Merkle-Damgard scheme. In short, we can concatenate the same string after the collision pair, and their MD5 digests would still be the same. We can make use of this to generate multiple messages yielding the same digest. Let $m_1$, $m_2$, $m'_1$ and $m'_2$ be 128-byte messages such that:

1. $\text{MD5}(m_1) = \text{MD5}(m_2)$ and
2. $\text{MD5}(m_1\ ||\ m'_1) = \text{MD5}(m_1\ ||\ m'_2)$.

Then the below equality holds:

\[\text{MD5}(m_1\ ||\ m'_1) = \text{MD5}(m_1\ ||\ m'_2) = \text{MD5}(m_2\ ||\ m'_1) = \text{MD5}(m_2\ ||\ m'_2).\]

What can be done? One more property on protobuf!

Essentially we can generate $m'_1$ and $m'_2$ which respectively "overwrites the move with scissors" and "does nothing". This is the same as what we did previously: $m_1$ overwrote the move with paper and $m_2$ did nothing... and we have a 148-byte prefix for Unicoll!

1a 07 00 00 00 00 00 00 00 18 01 0a 05 04 05 06 07 08 1a 6c 11 e1 00 b5 d6 e0 e8 59 d2 1a ba f6
45 c7 64 92 91 43 f4 6c 46 11 cd 78 ac 72 d5 49 7f dd ec 8b 6f 18 a7 9f 5e 55 1a 49 90 0b 29 6e
23 8b 8e 23 06 62 2a 07 ec be 56 14 39 02 91 60 ce c6 60 be 16 35 74 a3 b5 78 11 21 3b e6 2d d8
2a bb cc aa 9b 55 89 bc 43 a8 cc 5c 97 0f 92 25 f6 72 0b 99 0f 47 2e e0 71 15 4e 97 85 e0 23 86

1a 07 00 00 00 00 00 00 00 18 02 0a 05 04 05 06 07 08 1a 6c

There is the collision pair generated, and both of the messages have the MD5 digest d65c76e692c2b4c81b05a20928375fc3:

1a 07 00 00 00 00 00 00 00 18 01 0a 05 04 05 06 07 08 1a 6c 11 e1 00 b5 d6 e0 e8 59 d2 1a ba f6
45 c7 64 92 91 43 f4 6c 46 11 cd 78 ac 72 d5 49 7f dd ec 8b 6f 18 a7 9f 5e 55 1a 49 90 0b 29 6e
23 8b 8e 23 06 62 2a 07 ec be 56 14 39 02 91 60 ce c6 60 be 16 35 74 a3 b5 78 11 21 3b e6 2d d8
2a bb cc aa 9b 55 89 bc 43 a8 cc 5c 97 0f 92 25 f6 72 0b 99 0f 47 2e e0 71 15 4e 97 85 e0 23 86

1a 07 00 00 00 00 00 00 00 18 02 0a 05 04 05 06 07 08 1a 6c 37 41 76 c6 67 9c 61 22 b6 c0 7c e8
47 80 c9 13 9b 01 66 db 88 46 2e 6a cc fe ea d5 5a 12 ff f1 4d a6 c4 9d ef c4 cb 40 62 b4 90 cf
92 3f 36 ec 96 0f c9 54 43 00 e5 a9 3e 4d df f8 99 92 77 54 1a 27 64 00 79 f2 52 2c 48 39 6f b9
a6 ef 7d c3 07 4d 40 c3 8b d5 73 42 37 3f 6d e1 b5 50 67 87 ed 32 cd 23 75 f5 15 05 51 75 51 70

1a 07 00 00 00 00 00 00 00 18 01 0a 05 04 05 06 07 08 1a 6c 11 e1 00 b5 d6 e0 e8 59 d2 1a ba f6
45 c7 64 92 91 43 f4 6c 46 11 cd 78 ac 72 d5 49 7f dd ec 8b 6f 18 a7 9f 5e 55 1a 49 90 0b 29 6e
23 8b 8e 23 06 62 2a 07 ec be 56 14 39 02 91 60 ce c6 60 be 16 35 74 a3 b5 78 11 21 3b e6 2d d8
2a bb cc aa 9b 55 89 bc 43 a8 cc 5c 97 0f 92 25 f6 72 0b 99 0f 47 2e e0 71 15 4e 97 85 e0 23 86

1a 07 00 00 00 00 00 00 00 19 02 0a 05 04 05 06 07 08 1a 6c 37 41 76 c6 67 9c 61 22 b6 c0 7c e8
47 80 c9 13 9b 01 66 db 88 46 2e 6a cc fe ea d5 5a 12 ff f1 4d a6 c4 9d ef c4 cb 40 62 b4 90 cf
92 3f 36 ec 96 0f c9 54 43 ff e4 a9 3e 4d df f8 99 92 77 54 1a 27 64 00 79 f2 52 2c 48 39 6f b9
a6 ef 7d c3 07 4d 40 c3 8b d5 73 42 37 3f 6d e1 b5 50 67 87 ed 32 cd 23 75 f5 15 05 51 75 51 70

And they are accordingly when decoded,

move = bytes.fromhex('00 00 00 00 00 00 00')   # bytes
move = 1                                       # enum, equivalent to "PAPER"
nonce_client = bytes.fromhex('04 05 06 07 08') # bytes
move = bytes.fromhex('11 e1 00 ... e0 23 86')  # bytes

move = bytes.fromhex('00 00 00 00 00 00 00')   # bytes
move = 2                                       # enum, equivalent to "SCISSORS"
nonce_client = bytes.fromhex('04 05 06 07 08') # bytes
move = bytes.fromhex('37 41 76 ... 75 51 70')  # bytes

# As a result:
move = 2 # SCISSORS
nonce_client = bytes.fromhex('04 05 06 07 08')

move = bytes.fromhex('00 00 00 00 00 00 00')   # bytes
move = 1                                       # enum, equivalent to "PAPER"
nonce_client = bytes.fromhex('04 05 06 07 08') # bytes
move = bytes.fromhex('11 e1 00 ... e0 23 86')  # bytes

move = bytes.fromhex('00 00 00 00 00 00 00')   # bytes
move = 0x08_07_06_05_04_05_0a_02               # fixed64
move = bytes.fromhex('37 41 76 ... 75 51 70')  # bytes

# As a result:
move = 1 # PAPER
nonce_client = bytes.fromhex('04 05 06 07 08')

Part VI: The final messages⌗

From above, we have $m_1\ ||\ m'_1$ and $m_1\ ||\ m'_2$. We can replace $m_1$ with $m_2$ to get four messages with the same digest. We can pick any move by concatenating different message chunks, as shown below:

Finally, we can concatenate the nonce_server and nonce_client to whatever we want. These are the final messages, with the assumption that nonce_server = ff...ff and nonce_client = 00...00:

We can now use $m_1$, $m_2$, $m'_1$ and $m'_2$ to win every single game and get the flag: hkcert22{bu7_wh0_u53s_md5_1n_2022}. Congratulations to @hoifanrd (short for Hoi Fan Road, or 海帆道) being the only solver of the challenge.