HKCERT CTF 2022 Postmortem (III): The Remaining Challenges
In the last part, I will include the two non-crypto challenges I wrote for HKCERT CTF 2022: Numbers go brrr and Minecraft geoguessr.
觀塘海濱音樂噴泉 / Numbers go brrr (Reverse)⌗
Challenge Summary⌗
This program is generating 100 sets of random numbers and they are asking me to send something back, in exchange for a flag. Can you figure out how to get them through?
nc HOST PORTAttachments: solve.py
There is a nc service, and we will be given some numbers upon connecting. We are asked to send something each time the 🥺 emoji appeared. From the description, we will be given the flag after sending correct responses 100 times.
On top of that, there is an attachment called solve.py:
from pwn import *
from z3 import *
from operator import add, mul
from functools import reduce
from rich.progress import track
import itertools
# TODO: change this to the remote service
r = process('./chall')
for _ in track(range(100)):
r.recvuntil('🔧 '.encode())
m, s, p, q = map(int, r.recvline().decode().split())
_s = Solver()
xs = [Int(f'x_{i}') for i in range(m)]
subss = [Int(f'ss_{i}') for i in range(m)]
subps = [Int(f'ps_{i}') for i in range(m)]
# The base conditions
for i in range(1, m):
_s.add(xs[i-1] <= xs[i])
for i in range(0, m):
_s.add(Not(xs[i] <= 0))
for i in range(0, m):
_s.add(xs[i] < q)
for i, j in itertools.product(range(0, m), repeat=2):
_s.add(Implies(i != j, xs[i] != xs[j]))
# The "s" and "p" requirements
_s.add(subss[0] == xs[0])
_s.add(subps[0] == xs[0])
for i in range(m-1):
_s.add(subss[i+1] == subss[i] + (i+2)*xs[i+1])
_s.add(subps[i+1] == subps[i] * (i+2)*xs[i+1])
_s.add(subss[m-1] % q == s)
_s.add(subps[m-1] % q == p)
assert _s.check() == sat
md = _s.model()
x0s = [md.evaluate(xs[i]) for i in range(m)]
r.sendlineafter('🥺 '.encode(), ' '.join(map(str, x0s)).encode())
print(r.recvline().strip().decode())solve.py? Hear me out… This is not a mistake.
Solution⌗
Part I: An unintended solution⌗
To solve the challenge, we can just run solve.py and it is done. Just kidding, it is impossible to solve the challenge in this way. Let's read the solve script and see what is going on.
Part II: Understanding the solve script⌗
There are 100 rounds in total. In each round, we will receive four numbers $m, s, p, q$ from the server and we need to find $(x_1, x_2, ..., x_m)$ satisfying the base conditions:
- $x_1 \leq x_2 \leq ... \leq x_m$,
- $0 < x_i < q$ for $i = 1, 2, ..., m$, and
- For any $i \neq j$, $x_i \neq x_j$.
In addition, the $m$-tuple needs to satisfy the "s" and "p" requirements (short for sum and product, respectively):
- $x_1 + 2 x_2 + ... + m x_m \equiv s \ (\text{mod}\ q)$, and
- $x_1 \cdot 2 x_2 \cdot ... \cdot m x_m \ \equiv p \ (\text{mod}\ q)$.
That is it! We can deduce the actual problem statement from the solution script, and we can simplify the base condition:
\[0 < x_1 < x_2 < ... < x_m < q.\]
We can also simplify the product requirement:
\[x_1 \cdot x_2 \cdot ... \cdot x_m \equiv p' \quad (\text{mod}\ q),\]
where $p' \equiv p \cdot (1 \cdot 2 \cdot ... \cdot m)^{-1}\ \text{mod}\ q$.
Part III: Reducing an undetermined system⌗
If we consider only the sum and product requirements, there are $m$ unknowns and two equations. If $m > 2$, then the system is underdetermined:
\[\begin{cases} x_1 + 2 x_2 + ... + m x_m & \equiv s \quad (\text{mod}\ q) \\ x_1 \cdot x_2 \cdot ... \cdot x_m& \equiv p' \quad (\text{mod}\ q) \end{cases}\]
This is easy. We can just assume that $x_1 = 1, x_2 = 2, ..., x_{m-2} = m-2$. What is remaining in the equations are:
\[\begin{cases} 1 + 2 \cdot 2 + ... + (m-2) \cdot (m-2) + (m-1) x_{m-1} + m x_m & \equiv s \quad (\text{mod}\ q) \\ 1 \cdot 2 \cdot ... \cdot (m-2) \cdot x_{m-1} \cdot x_m & \equiv p' \quad (\text{mod}\ q) \end{cases},\]
which is equivalent to
\[\begin{cases} (m-1) x_{m-1} + m x_m & \equiv s' \quad (\text{mod}\ q) \\ x_{m-1} \cdot x_m & \equiv p'' \quad (\text{mod}\ q) \end{cases}.\]
Here $s' = s - [1 + 2^2 + ... + (m-2)^2]\ (\text{mod}\ q)$ and $p'' = p' \cdot [1 \cdot 2 \cdot ... \cdot (m-2)]^{-1} \ (\text{mod}\ q)$.
Now we have a different objective: Find $m-2 < x_{m-1} < x_m < q$ such that the above system holds. Although the range of values are a little bit stricter, it is still easy to find a solution set.
Part IV: Solving a system of two equations, modulo prime $q$⌗
From the two equations, we can just rewrite the sum condition:
\[(m-1) \cdot x_{m-1} \equiv s - m \cdot x_m \quad (\text{mod}\ q).\]
Substituting the above to the product condition, we have
\[\begin{aligned} & (s - m \cdot x_m) \cdot x_m \equiv (m-1) \cdot p'' \quad (\text{mod}\ q) \\ & \Longrightarrow m \cdot {x_m}^{2} - s \cdot x_m + (m-1) \cdot p'' \equiv 0 \quad (\text{mod}\ q), \end{aligned}\]
which is a quadratic congruence in $x_m$. To solve the equation, we will first reduce it into the form $u^2 \equiv b \ (\text{mod}\ q)$.
This is simple. We are essentially completing the square in modulo $q$:
\[\begin{aligned} & m \cdot {x_m}^{2} - s \cdot x_m + (m-1) \cdot p'' \equiv 0 \quad (\text{mod}\ q) \\ & \Longrightarrow {x_m}^{2} - (s \sdot m^{-1}) \cdot x_m + (m-1) \cdot m^{-1} \cdot p'' \equiv 0 \quad (\text{mod}\ q) \\ & \Longrightarrow {x_m}^{2} - 2 \cdot [s \sdot (2m)^{-1}] \cdot x_m + (m-1) \cdot m^{-1} \cdot p'' \equiv 0 \quad (\text{mod}\ q) \\ & \Longrightarrow {x_m}^{2} - 2 \cdot [s \sdot (2m)^{-1}] \cdot x_m + [s \sdot (2m)^{-1}]^2 \equiv [s \sdot (2m)^{-1}]^2 - (m-1) \cdot m^{-1} \cdot p'' \quad (\text{mod}\ q) \\ & \Longrightarrow [x_m - s \cdot (2m)^{-1}]^2 \equiv [s \sdot (2m)^{-1}]^2 - (m-1) \cdot m^{-1} \cdot p'' \quad (\text{mod}\ q) \end{aligned}\]
With $u = x_m - s \cdot (2m)^{-1}$ and $b = [s \sdot (2m)^{-1}]^2 - (m-1) \cdot m^{-1} \cdot p''$, we have the equation $u^2 \equiv b \ (\text{mod}\ q)$. To find the values of $u$, we can apply the Tonelli-Shanks algorithm. After that, we can compute $x_m$ from $u + s \cdot (2m)^{-1}$ and obtain $x_{m-1}$ easily.
It is not uncommon that either no solutions exist, or $m-2 < x_{m-1} < x_m < q$ does not hold. In these cases, we can use another set of values for $(x_1, x_2, ..., x_{m-3}, x_{m-2})$ such that $x_{m-2}$ is small enough. After that, we can find $x_{m-1}$ and $x_m$ with the above approach and stop when we have $x_{m-2} < x_{m-1} < x_m < q$.
With that implemented, we can finally pass the 100 rounds. We will eventually get the flag: hkcert22{z3_i5_4n_sw1s5_4rmy_kn1f3_bu7_1t_i5_n0t_alw4y5_f4s7}.
CGA 香港電競館 / Minecraft Geoguessr (Misc)⌗
Challenge Summary⌗
Do you know Rainbolt? If you send him a photo, he could immediately tell you where it was taken in.
Can you do the same in the Minecraft world?
Note: If you are desperate, you can watch Rainbolt's most insane geoguessr moments, or LiveOverflow's video series on Minecraft Hacking.
By the way, the map is generated with Minecraft 1.17.1. With that said, you may be unable to look for the better caves.
Attachments: whereami.png
We are given a web service that receives 5-tuples $(x, y, z, \theta, \varphi)$ from players, where $x, y, z$ are the coordinates, and $\theta$ and $\varphi$ are respectively the yaw and pitch. We will receive a screenshot taken in the specified location. Also, $-20000 \leq x, z \leq 20000$, $0 \leq y \leq 256$, $-180 \leq \theta \leq 180$, $-90 \leq \varphi \leq 90$.
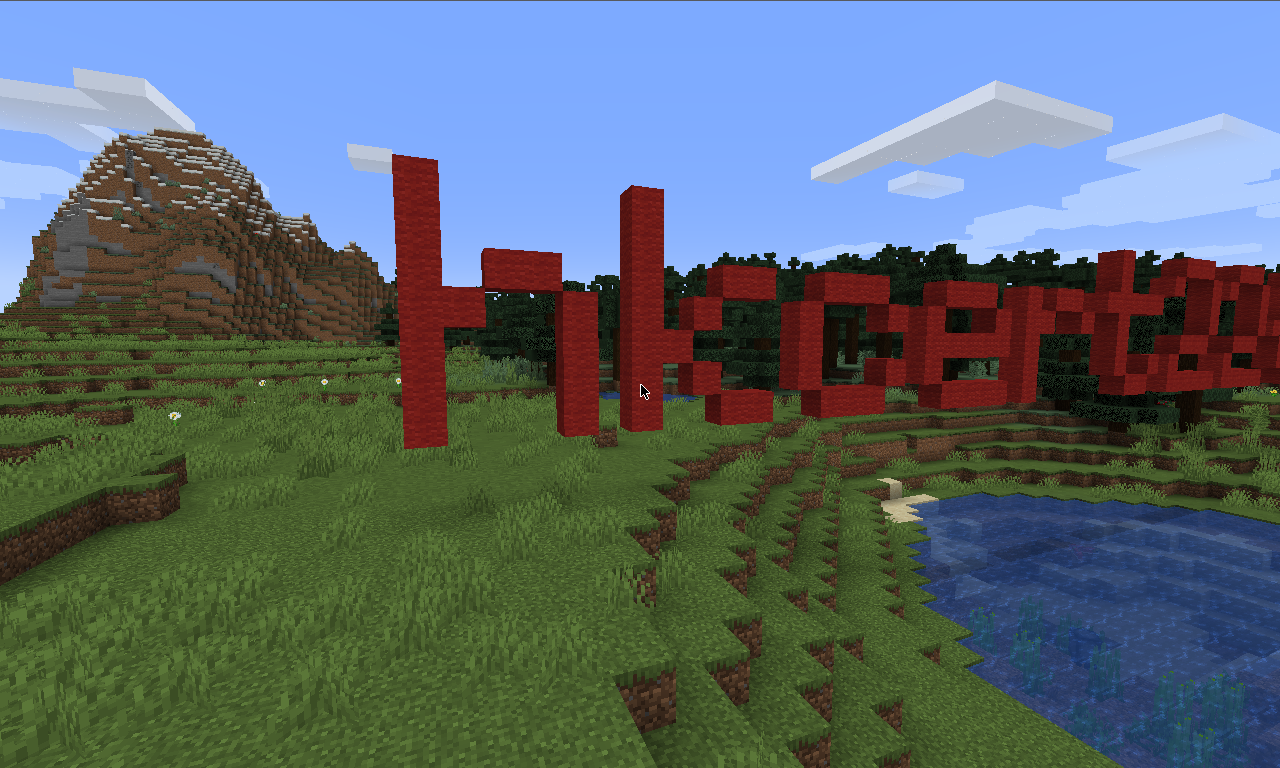
On the other hand, we are also given the below screenshot, where only the prefix of the flag hkcert22{ is shown. The objective is to recover the flag.

Solution⌗
Part I: Doing some OSINTs with the screenshot⌗
The most attractive thing about the screenshot is the prefix of the flag. But what else can we retrieve from it?
Let's talk about Minecraft history. @SimplySarc uploaded a video in 2012 that showed that the rotation of lily pads is only dependent on their position. Also, snapshot 14w27b (for version 1.8) was released eight years ago. Below is an excerpt of the patch notes:
The block state files now support an array of models allowing for random models. As a result of this, grass blocks, dirt, sand, red sand, stone, netherrack, bedrock, and TNT all have their top texture randomly rotated.
When they say "random", it is dependent on the position like the lily pads. With that said, we can collect information from the grass blocks' rotation to find its coordinates. Surprising, right?
A legendary GeoGuessr player, @georainbolt, once said why touch grass when you can study grass. We can do the same in the Minecraft world. Now, look at a grass block. There are four rotations (rotated 0º, 90º, 180º and 270º).

Well, I know this is probably the most difficult part -- labelling. Let's identify the orientations of some grass blocks in the screenshot:
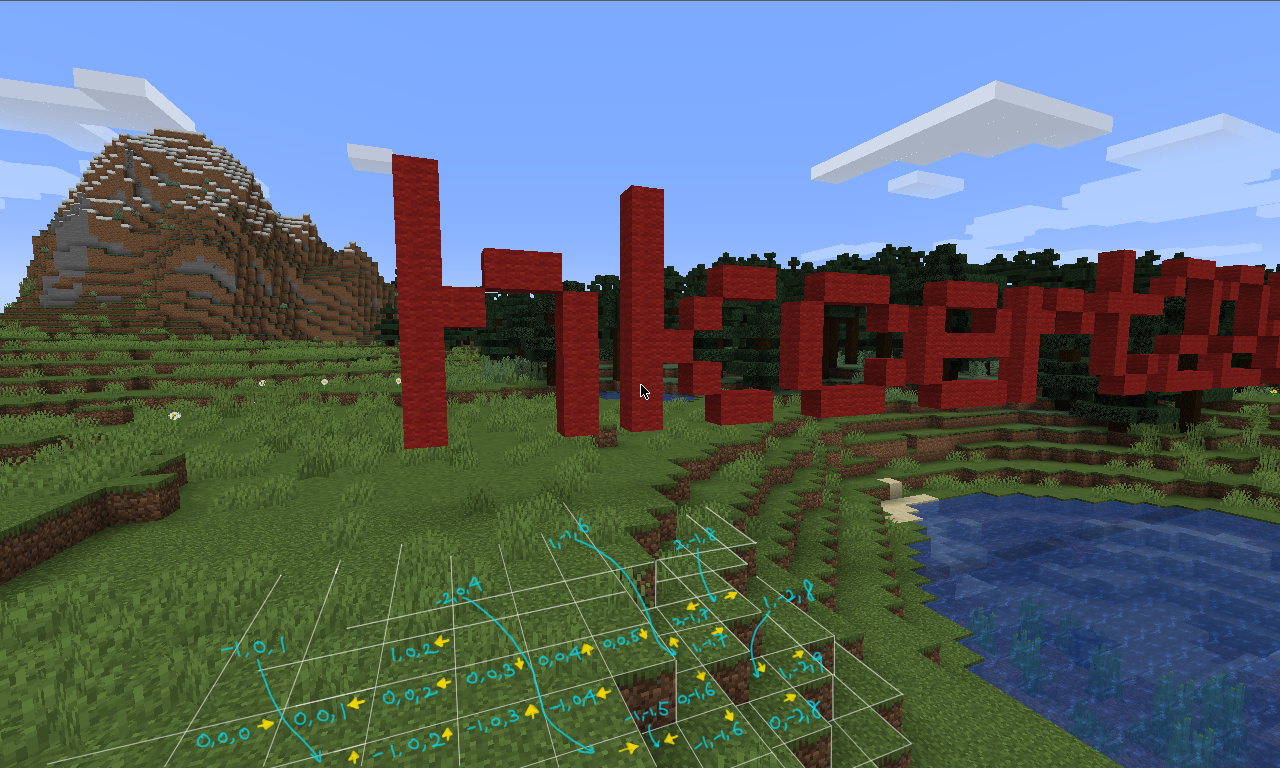
From above, I collected the rotations of 22 grass blocks.
| (0, 0, 0) ➡️ |
(0, 0, 1) ⬅️ |
(-1, 0, 1) ⬆️ |
(1, 0, 2) ⬅️ |
(0, 0, 2) ⬅️ |
(-1, 0, 2) ⬆️ |
| (0, 0, 3) ⬇️ |
(-1, 0, 3) ⬆️ |
(0, 0, 4) ⬆️ |
(-1, 0, 4) ⬅️ |
(-2, 0, 4) ➡️ |
(0, 0, 5) ⬇️ |
| (-1, -1, 5) ⬅️ |
(1, -1, 6) ⬆️ |
(0, -1, 6) ⬇️ |
(-1, -1, 6) ⬇️ |
(2, -1, 7) ⬅️ |
(1, -1, 7) ➡️ |
| (2, -1, 8) ➡️ |
(1, -2, 8) ⬇️ |
(0, -2, 8) ➡️ |
(1, -2, 9) ➡️ |
||
It is very unlikely (with the probability being $1/4^{22}$) for a patch of 22 blocks that has the same rotations. Thus, there should be only one matching coordinate if we scan through every block in $-20000 \leq x, z \leq 20000$ and $0 \leq y \leq 256$. Below is the pseudo-code that we are going to implement:
From above, we know (x0+0, y0+0, z0+0) is pointing rightwards and
(x0+0, y0+0, z0+1) is pointing leftwards and ... and
(x0+1, y0-2, z0+9) is pointing rightwards
for some (x0, y0, z0).
For each -20000 <= x <= 20000, 0 <= y <= 256, -20000 <= z <= 20000:
If (x+0, y+0, z+0) is pointing rightwards and
(x+0, y+0, z+1) is pointing leftwards and ... and
(x+1, y-2, z+9) is pointing rightwards, then:
(x, y, z) are the coordinates we want!A final problem is we don't know which direction the player is facing. Luckily, as there are only four possibilities, we can simply exhaust them all. By the way, some players can identify the player's orientation, so they can speed up their algorithm (at least) four times faster than our brute-forcing approach!
Part II: Reverse engineering Minecraft⌗
hacker mann uploaded a video in 2019 discussing a way to recover the coordinates from block rotation. The below code is a simplified, yet accurate way to compute the texture rotation of a block. It is a combination of multiple functions:
// An Java implementation of the `getRotation`
public static long getRotation(int x, int y, int z) {
// Math#getSeed
long l = (long)(x * 3129871) ^ (long)z * 116129781L ^ (long)y;
l = l * l * 42317861L + l * 11L;
long seed = l >> 16;
// ModelBlockRenderer#tesselateWithAO
Random random = new Random(seed);
// WeightedBakedModel#getQuads
return Math.abs(random.nextLong()) % 4;
}Hereby Random is an implementation from the JDK, which can be referenced from their source code. To summarize, the random is a linear congruential generator (LCG), with the initial state, $s_0$, being
\[s_0 := (\text{seed} \oplus \text{5DEECE66D}_{16}) \ \text{mod}\ 2^{48}.\]
The subsequent states $s_1, s_2, ...$ are all 48 bits and deduced by the current state:
\[s_{i+1} := (\text{5DEECE66D}_{16} \cdot s_i + \text{B}_{16}) \ \text{mod} \ 2^{48}.\]
If the current state is $s_i$, then the output of nextInt() would be $y_i := \lfloor{ s_{i+1} / 2^{16} \rfloor}$. Simply put, it is the top 32 bits of the next state. Also, nextLong() is defined by the below code snippet:
public long nextLong() {
return ((long)(next(32)) << 32) + next(32);
}Part III: Preparing a program for brute-forcing⌗
From the above implementation, we know that the seed is derived from the coordinates of the block. This is my translation in Golang which optimized the algorithm a bit:
func getRotation(x, y, z int) int32 {
/*
long l = (long)(x * 3129871) ^ (long)z * 116129781L ^ (long)y;
l = l * l * 42317861L + l * 11L;
long seed = l >> 16;
*/
x2 := int(int32(x * 3129871))
z2 := z * 116129781
l := x2 ^ y ^ z2
l = l * (l*42317861 + 11) // l = l*l*42317861 + l*11
seed := l >> 16
/*
Random random = new Random(seed);
*/
seed ^= 0x5DEECE66D
/*
return Math.abs(random.nextLong()) % 4;
*/
v := int32((seed*0xBB20B4600A69 + 0x40942DE6BA) >> 16)
if v < 0 {
v = -v
}
return v & 3
}Well, I didn't compare the running times of the implementations in Golang and Java, which may be similar. I use Golang simply because I rarely code in Java anyway.
After that, what is missing is just a routine that exhausts the whole search space, and includes the block rotation we found from the screenshot. We can decrease the running time with multithreading, too.
I implemented my solution using Golang. With 8 threads and search space being $-20000 \leq x, z \leq 20000$ and $64 \leq y < 100$, it only takes 6 minutes to run.
The coordinates we found are $(16551, 67, 4170)$. We can now ask our intern to teleport nearby for the whole flag: hkcert22{s33d_cr34kin9_1s_r3ver53_4nd_cryp70_com61ned}.
Part IV: Reducing the search time⌗
There are two notable ways to reduce the search time, provided by the contestants @HotDawggyy and Gameboy612. We can recover the coordinates in less than ten seconds with either of the two improvements implemented. This is remarkable!
Hey, look at the clouds!⌗
@HotDawggyy looked at the cloud and found that the $z$-coordinate should be roughly 4180 when taken modulo 6144. Assuming that the absolute error is 64 blocks, i.e., $4180-64 < z\ \text{mod}\ 6144 < 4180+64$. This reduced the search space by 98.0%.

Look at the water, too!⌗
On the other hand, Gameboy612 reduced the search space by determining the sea level. If we assume that the pool of water is at sea level (i.e., $y = 62$), we can just fix the $y$-coordinate to one single value. This reduces the search space by 97.2%.
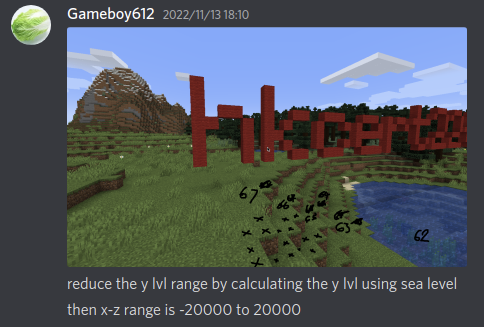
Finally, it is impressive that Gameboy612 is a secondary school student and their team got the first blood 🩸 of this challenge. Congratulations!