HKCERT CTF 2023 Postmortem (II): Harder Crypto Challenges

In the second part of the series, I will cover four cryptography challenges: baDES, Maybe Someday, Cipher Bridging Service and RSA Triooo. Interestingly, most of them are somehow “plagiarized” from the other CTFs.
baDES⌗
Challenge Summary⌗
DES, published as an official Federal Information Processing Standard in 1977, is considered bad in 2023. We will slightly change the cipher and attack that together!
https://HOST:PORT/
Note: There is a guide for this challenge here.
Attachments: bades.zip
In this challenge, we are given an slightly modified Data Encryption Standard (denoted by DES'). Additionally, we are given the two oracles:
encrypt_flagencrypts the flag using DES'-CBC.encryptencrypts an arbitrary message using DES'-CBC.
Additionally, the initialization vector of the encryption calls are fixed. The goal is to retrieve the flag using the above oracle calls.
Solution⌗
How is the cipher being modified?⌗
The only change to the cipher is the values of the left shifts for the key schedule, __left_rotations:
- [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
+ [16, 25, 8, 1, 7, 13, 3, 4, 0, 24, 25, 15, 21, 27, 20, 3]
DES is a Feistel cipher, where the plaintext will go through 16 rounds of Feistel function with 16 subkeys, $k_1, k_2, …, k_{16}$. The subkeys are derived only with the key and the left shifts, illustrated below:
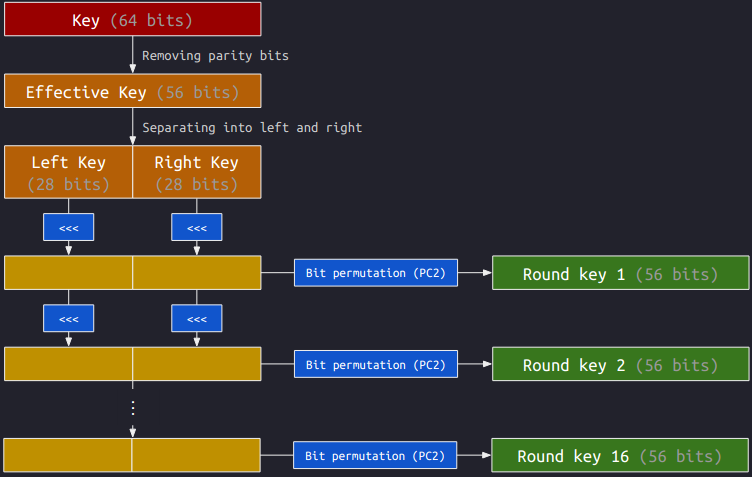
The shifts of the intermediate keys (the blocks in dark yellow) are accumulated. Since both the left and right keys are 28 bits, the partial key would become itself after shifting 28 bits. The following table shows the accumulated shifts before PC2:
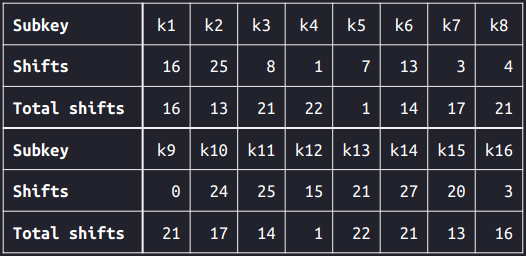
From the table, we can see that the accumulated shifts for $k_1$ and $k_{16}$ are the same. This would imply that $k_1 = k_{16}$. Similarly, we have $k_2 = k_{15}$, $k_3 = k_{14}$, …, $k_8 = k_9$.
Every key is a weak key⌗
We can claim that every key is a weak key with the above property. Therefore we have $\text{Encrypt}_k = \text{Decrypt}_k.$ This mean that the encryption function is exactly the decryption function. In this way, if we encrypt a ciphertext, it actually decrypts it. But why?
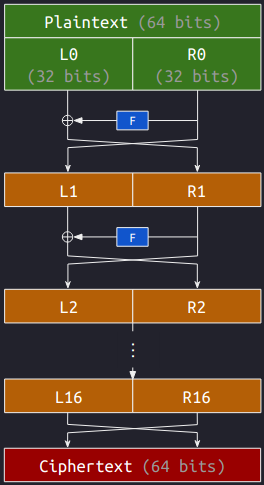
Let’s look at the Feistel rounds of DES above, where we respectively let $(L_0, R_0)$ and $(R_{16}, L_{16})$ be the plaintext and the ciphertext. We then have
$$L_{i + 1} = R_i \quad \text{and} \quad R_{i+1} = L_i \oplus F(R_i, k_{i+1}).$$
Now we let $(L'_0, R'_0)$ to be the ciphertext for $(L_0, R_0)$, i.e., $L'_0 = R_{16}$ and $R'_0 = L_{16}$. Then we have
$$\begin{cases}\begin{aligned} L'_1 &= R'_0 = L_{16} = R_{15} \\ R'_1 &= L'_0 \oplus F(R'_0, k_1) = R_{16} \oplus F(L_{16}, k_{16}) = L_{15}. \end{aligned}\end{cases}$$
Repeating the process, we eventually have $L'_{16} = R_0$ and $R'_{16} = L_0$. Therefore, the corresponding ciphertext for $(L_{16}, R_{16})$ is $(L_0, R_0)$.
$$(L_0, R_0) \xrightarrow{\text{Encrypt}} (L_{16}, R_{16}) \xrightarrow{\text{Encrypt}} (L_0, R_0).$$
ECB and CBC⌗
The above property happens for a single block of the DES' cipher. In this challenge, the messages are encrypted using the cipher block chaining (CBC) mode. Hence if we have a message $(m_1, m_2, …)$ where $m_i$ is the $i$-th message block, then we have
$$c_i = \text{Encrypt}(c_{i-1} \oplus m_i)$$
for $i = 1, 2, …$. Here $c_0$ is the initialization vector.
To recover $m_1$, we can encrypt $m'_1 := c_0 \oplus c_1$ using the oracle. The corresponding ciphertext, $c'_1$, would be
$$\begin{aligned} c'_1 &= \text{Encrypt}(c_0 \oplus m'_1) = \text{Encrypt}(c_0 \oplus c_0 \oplus c_1) \\ &= \text{Encrypt}(c_1) = \text{Decrypt}(c_1) = c_0 \oplus m_1. \end{aligned}$$
Hence, we can recover $m_1$ by computing $c_0 \oplus c'_1$. We can further recover $m_i$ for the subsequent $i$’s by encrypting $m'_1 = c_0 \oplus c_i$, where the corresponding ciphertext $c'_1$ is
$$\begin{aligned} c'_1 &= \text{Encrypt}(c_0 \oplus m'_i) = \text{Encrypt}(c_0 \oplus c_0 \oplus c_i) \\ &= \text{Encrypt}(c_i) = \text{Decrypt}(c_i) = c_{i-1} \oplus m_i, \end{aligned}$$
and recover $m_i$ using $c_{i-1} \oplus c'_1$. With this, we can recover the full flag:
hkcert23{DES_c4n_6e_34s1ly_d0wngr4d3d_6y_ch4ng31ng_l1t71e_th1n9s}
Maybe Someday⌗
Challenge Summary⌗
Wait, isn’t this the challenge from Google CTF 2022? As the challenge author, Mystiz has even compiled the writeup…
The source code is slightly different. Never mind.
nc HOST PORTAttachments: maybe-someday.zip
A set of Paillier keys is generated when connected to the server. The players are given the public key $(n, g)$. Also, we are also given an encrypted flag, $c_0$, which is padded in PKCS#1v1.5.
We are given an oracle for ciphertext $c$. The server will decrypt $c$, unpad and send the least significant bit of the message to the player. If there is an exception (for instance, invalid padding), the program would terminate. Finally, the goal is to recover the flag.
Solution⌗
Let $m_0$ be a flag padded in PKCS#1v1.5 and $c_0$ is a corresponding ciphertext. We are only given the ciphertext $c_0$.
$$m_0 = \texttt{00} \ \texttt{02} \ \texttt{[PADDING]} \ \texttt{00} \ || \ \texttt{68} \ \texttt{6b} \ \texttt{63} \ \texttt{65} \ \texttt{72} \ \texttt{74} \ \dots.$$
Here $\texttt{68} \ \texttt{6b} \ \texttt{63} \ \texttt{65} \ \texttt{72} \ \texttt{74} \ \dots$ is the flag, and we know it starts with hkcert.
Since we are given the LSB oracle, it is evident that we can retrieve $m_0 \ \text{mod}\ 2$ by simply sending $c_0$ to the oracle. Suppose that $m_0 = 2m_1 + b_0$ (hereby $b_0$ is the LSB of $m_0$), we can get a ciphertext of $\mathcal{E}(m_1)$ using the homomorphic properties. Mathematically,
$$\begin{aligned} \mathcal{E}(m_1) &= \mathcal{E}(2^{-1} \cdot (m_0 - b_0)) = \mathcal{E}(m_0 - b_0)^k \\ &= [\mathcal{E}(m_0) \cdot \mathcal{E}(-b_0)]^k, \end{aligned}$$
where $k = 2^{-1} \ \text{mod}\ n$. This is equivalent to make the new plaintext to be $\lfloor m_0/2\rfloor$, thus effectively move the second bit to the LSB. Unfortunately, the padding will be no longer valid.
$$m_1 = \begin{cases} \texttt{00} \ \texttt{01} \ \texttt{[PADDING]} \ \texttt{00} \ || \ \texttt{34} \ \texttt{35} \ \texttt{b1} \ \texttt{b2} \ \texttt{b9} \ \texttt{3a} \ \dots & \text{if} \ p_k \equiv 1 \ (\text{mod}\ 2) \\ \texttt{00} \ \texttt{01} \ \texttt{[PADDING]} \ \texttt{80} \ || \ \texttt{34} \ \texttt{35} \ \texttt{b1} \ \texttt{b2} \ \texttt{b9} \ \texttt{3a} \ \dots & \text{otherwise} \end{cases}$$
$m_1$, which is currently $\lfloor m_0/2\rfloor$, is no longer PKCS#1v1.5-compliant because of the two reasons. The second byte of $m_1$ became $\texttt{01}$, which no longer equals $\texttt{02}$. Also, the null bytes between the padding the message will be replaced by a $\texttt{80}$ if $p_k$ is odd.
To solve the first problem, we should add $256^{254}$ to $m_1$. Now the second byte would became $\texttt{02}$ again.
$$m_1 = \begin{cases} \texttt{00} \ \texttt{02} \ \texttt{[PADDING]} \ \texttt{00} \ || \ \texttt{34} \ \texttt{35} \ \texttt{b1} \ \texttt{b2} \ \texttt{b9} \ \texttt{3a} \ \dots & \text{if} \ p_k \equiv 1 \ (\text{mod}\ 2) \\ \texttt{00} \ \texttt{02} \ \texttt{[PADDING]} \ \texttt{80} \ || \ \texttt{34} \ \texttt{35} \ \texttt{b1} \ \texttt{b2} \ \texttt{b9} \ \texttt{3a} \ \dots & \text{otherwise} \end{cases}$$
However, it is tricky to force the byte between the padding and the message to be zero. Fortunately, we know that the flag starts with h. By replacing the h to a null byte (mathematically, subtract $\texttt{68} \ \texttt{00} \ … \ \texttt{00}$ from $m_0$), we are have 16 unset bits after the padding, which guaranteeded that there will be a null byte.
$$m_1 = \begin{cases} \texttt{00} \ \texttt{02} \ \texttt{[PADDING]} \ \texttt{00} \ || \ \texttt{00} \ \texttt{35} \ \texttt{b1} \ \texttt{b2} \ \texttt{b9} \ \texttt{3a} \ \dots & \text{if} \ p_k \equiv 1 \ (\text{mod}\ 2) \\ \texttt{00} \ \texttt{02} \ \texttt{[PADDING]} \ \texttt{80} \ || \ \texttt{00} \ \texttt{35} \ \texttt{b1} \ \texttt{b2} \ \texttt{b9} \ \texttt{3a} \ \dots & \text{otherwise} \end{cases}$$
However, we need the length of the flag before forcing its first character to a null byte. To retrieve the flag length, we can simply add $\texttt{01}$, $\texttt{01} \ \texttt{00}$, $\texttt{01}\ \texttt{00}\ \texttt{00}$, … to the plaintext, until we are kicked from the server. We are kicked because the plaintext became $\texttt{00}\ \texttt{02}\ \texttt{[PADDING]}\ \texttt{01}\ || \ \texttt{[FLAG]}$, which the null byte between the padding and the message has been replaced.
After all, this is the flow to recover the flag:
- Connect to the server. Add $\texttt{01}$, $\texttt{01} \ \texttt{00}$, $\texttt{01}\ \texttt{00}\ \texttt{00}$ and so on to the plaintext using the homomorphic property. Suppose that we are kicked after adding $\texttt{01} \ \texttt{00} \ \texttt{00} \ \dots \ \texttt{00}$ (one $\texttt{01}$ followed by $l$ $\texttt{00}$’s) to the plaintext. In that way, we know that the flag is $l$ character long.
- Reconnect to the server. Let $c_0$ be the encrypted flag.
- Update $c_0$ using the homomorphic property so that the corresponding plaintext becomes $\texttt{00} \ \texttt{02} \ \texttt{[PADDING]} \ \texttt{00} \ || \ \texttt{00} \ \texttt{6b} \ \texttt{63} \ \texttt{65} \ \texttt{72} \ \texttt{74} \ \dots$, and set $m \leftarrow \texttt{68} \times 256^{l-1}$.
- For $i = 0, 1, 2, …, 8l-9$, do the following
- Call the LSB oracle with the current $c_0$, and denote the output by $b$.
- Update $m \leftarrow m + 2^i \cdot b$.
- Update $c_0$ so that the corresponding plaintext is halved. After that, update $c_0$ so that the plaintext starts with $\texttt{00} \ \texttt{02}$.
- Finally, $m$ is now the flag.
hkcert23{wh0_w0u1d_ev3r_l34k_4_b1t_fr0m_th3_p1a1n73xt_1n_2023?}
Cipher Bridging Service⌗
Challenge Summary⌗
I implemented a cipher switching service (totally not the one from TSJ CTF 2022) and served as a bridge between symmetric and asymmetric ciphers. Can you find my secret on the bridge?
nc HOST PORTAttachments: cipher-bridging-service.zip
In this challenge, we are given a “cipher bridging service”. When connected to the service, a 16-byte AES key and a 2048-bit RSA key are generated. It will be used in the entire connection. Define the four functions:
- $\text{AESEncrypt}(m)$ generates a 16-byte $\nu$, pad the message $m$ and encrypt the padded message in AES-CBC with IV being $\nu$. Prepend $\nu$ before the ciphertext and return.
- $\text{AESDecrypt}(c)$ takes the first 16-byte as $\nu$, decrypt the remaining bytes with AES-CBC with IV being $\nu$. Unpad the message and return.
- $\text{RSAEncrypt}(m)$ encrypts the message with RSA.
- $\text{RSADecrypt}(c)$ decrypts the message with RSA.
There are two type of calls:
- We can send a $c$ (not longer than 256 bytes). The server computes and returns $\text{RSAtoAES}(c) := \text{AESEncrypt}(\text{RSADecrypt}(c))$, and
- We can send a $c$ (not longer than 288 bytes). The server computes and returns $\text{AEStoRSA}(c) := \text{RSAEncrypt}(\text{AESDecrypt}(c))$.
Notably, the program would terminate when there are any exceptions (e.g. invalid padding). The server will generate $\text{secret}$ (which is composed of 128 hex characters) and return $\text{AESEncrypt}(\text{secret})$. The goal is to retrieve the secret in 3999 calls.
Solution⌗
Leaking an arbitrary AES-ECB block⌗
Suppose that we want to recover $m$ such that $c = \text{AES-ECB}(m)$.
We can obtain $\text{AESEncrypt}(0)$ by calling $\text{RSAtoAES}(0)$. The ciphertext will be of 32 bytes, a 16-byte IV $c_0$ followed by a 16-byte ciphertext $c_1$. Here
$$c_1 = \text{AESECBEncrypt}(c_0 \oplus \texttt{000f0f…0f}).$$
Imagine we have a AES-encrypted ciphertext $\nu \ || \ c \ || \ c_0'\ || \ c_1$. The corresponding plaintext would be $\text{prefix} \ ||\ \heartsuit \ ||\ \text{suffix}$. Here we don’t know what $\heartsuit$ is, but it is fine to not care about that. Instead, $\text{prefix} = \nu \oplus m$ and $\text{suffix} = \texttt{000f0f…0f} \oplus c_0 \oplus c_0'$ are something that we want to look at.
To leak the first byte of $m$, we would want to set $\text{suffix} = \texttt{1010…10}$. If the first byte of $\text{prefix}$ is $\texttt{00}$, the unpadded plaintext would be of 31 bytes. That said, the AES-encrypted ciphertext is 48 bytes long (instead of 64 bytes). Hence, we can leak the first byte with 512 oracle calls:
- Let $\nu_0 = \texttt{0000…00}, \nu_1 = \texttt{0100…00}, …, \nu_{255} = \texttt{ff00…00}$.
- Let $c_0' = c_0 \oplus \texttt{000f…0f} \oplus \texttt{1010…10}$.
- Call the oracle for 256 times: $t_i := \text{AEStoRSA}(\nu_i \ || \ c \ || \ c_0' \ || \ c_1)$ for $i = 0, 1, …, 255$.
- Call the oracle for 256 times: $s_i := \text{RSAtoAES}(t_i)$ for $i = 0, 1, …, 255$.
- If $s_i$ is of 48-byte long (the remaining ones are of 64 bytes), then the first byte of $m$ is $i$.
Similarly, we can recover the second byte with another 512 oracle calls:
- Let $\nu_0 = m_0 \ || \ \texttt{00…00}, \nu_1 = m_0 \ || \ \texttt{01…00}, …, \nu_{255} = m_0 \ || \ \texttt{ff…00}$.
- Let $c_0' = c_0 \oplus \texttt{000f…0f} \oplus \color{yellow}{\texttt{0f0f…0f}}$.
- Call the oracle for 256 times: $t_i := \text{AEStoRSA}(\nu_i \ || \ c \ || \ c_0' \ || \ c_1)$ for $i = 0, 1, …, 255$.
- Call the oracle for 256 times: $s_i := \text{RSAtoAES}(t_i)$ for $i = 0, 1, …, 255$.
- If $s_i$ is of 48-byte long, then the second byte of $m$ is $i$.
We can repeat the process until the entire block is recovered.
Extending the above to leak the secret⌗
From above, we are able to recover a block with $256 \times 16 \times 2 = 8192$ calls. Fortunately, we know that the secret is composed of hex characters. Hence we can recover one byte of the secret in $16 \times 2 = 32$ calls, thus we can recover a block in $16 \times 16 \times 2 = 512$ calls.
The secret is composed 128 hex charcaters, which is broken down into 8 blocks. Overall, we need $512 \times 8 = 4096$ calls to fully recover the secret. This is slightly over the bound.
It is obvious that when a hex character is not equal to 0, 1, …, e, then it must be a f. We can then recover one byte of the secret in $15 \times 2 = 30$ calls. After all, we can recover a block with $15 \times 16 \times 2 = 480$ calls, thus recover the secret in $480 \times 8 = 3840$ calls.
Unintended solutions⌗
Although my solution does not require recovering the public modulus for RSA, having it recovered could lead to much simpler solutions. We can use two calls to recover $n$ (the modulus):
- $s_1 = \text{RSAtoAES}(2^{1024} - 1)$
- $t_1 = \text{AEStoRSA}(s_1)$
From above, we have $2^{1024} - 1 \equiv t_1\ (\text{mod}\ n)$, so $n$ is a factor of $2^{1024} - 1 - t_1$. Hence we can effectively recover $n$.
grhkm’s solution (2066 calls)⌗
Knowing the $n$, grhkm from Black Bacon uses the homomorphic property of RSA to get a ciphertext of $k \cdot m$ from a ciphertext of $m$.
Suppose $t$ is a RSA-encrypted ciphertext of $m$ such that $0 \leq m < 2^{128}$. We can obtain $t'$ such that it is the ciphertext of $k \cdot m$ by
$$t' \equiv k^e \cdot t \ (\text{mod}\ n).$$
We can obtain $s' := \text{RSAtoAES}(t')$ and compute its length and we can use it to check whether $k \cdot m < 2^{128b}$ for some integer $b$. This can be used to retrieve such largest $k$ using binary search. With $k$, we are able to recover the possible values of $m$.
hoifanrd’s solution (65 calls)⌗
hoifanrd from M*****’s Fan Club combined the homomorphic property RSA and delegated some brute-force offline. He is able to leak four characters of the secret with two oracle calls. After all, hoifanrd is able to retrieve the secret with 65 additional calls. You can read his writeup here.
Genni’s solution (2 calls)⌗
Genni from Tower of Hanoi had a solution that uses two additional oracle calls. Let $s_0 := \text{AESEncrypt}(\text{secret})$ and $s_0'$ be $s_0$ with the most significant bit flipped.
- $t_0 = \text{AEStoRSA}(s_0)$
- $t_0' = \text{AEStoRSA}(s_0')$
Since $s_0$ is AES-CBC encrypted, we can flip the first bit of $s_0$ and the corresponding plaintext would have the first bit flipped as well. Thus, the resulting plaintext would be $\text{secret}' := \text{secret} \oplus 2^{1023}$. Since $\text{secret}$ is composed of hexadecimal characters, the first bit must be unset. Thus $\text{secret}' = \text{secret} + 2^{1023}$.
In this way, we have $t_0 \equiv \text{secret}^e \ (\text{mod}\ n)$ and $t_0' \equiv (\text{secret} + 2^{1023})^e \ (\text{mod}\ n)$. If we let
$$\begin{aligned} \text{f}(x) &= x^e - t_0 \\ \text{g}(x) &= (x + 2^{1023})^e - t_0', \end{aligned}$$
we have $\text{f}(\text{secret}) = \text{g}(\text{secret}) = 0$ and thus $x - \text{secret}$ is a factor of both $\text{f}(x)$ and $\text{g}(x)$. Finally, we can recover $\text{secret}$ by computing $\text{GCD}(\text{f}(x), \text{g}(x))$.
RSA Triooo⌗
Challenge Summary⌗
Miss the challenges I made? Here comes a remastered version of RSA Trio!
nc HOST PORTAttachments: rsa-trio.zip
When connected to the server, three 1024-bit primes $p$, $q$ and $r$ are generated. Let $n_1 = pq$, $n_2 = qr$ and $n_3 = rp$ and three RSA public keys $(n_1, e)$, $(n_2, e)$, $(n_3, e)$ are constructed (here e = 65537 and $q < p < r$, i.e., $n_1 < n_2 < n_3$).
Let $\mathcal{E}(m)$ be the encryption function that returns the ciphertext $c$:
$$\begin{aligned} & s = m^e\ \text{mod}\ n_1 \\ & t = s^e\ \text{mod}\ n_2 \\ & c = t^e\ \text{mod}\ n_3, \end{aligned}$$
and $\mathcal{D}(c)$ be the decryption function that returns the message $m$:
$$\begin{aligned} & t = c^d\ \text{mod}\ n_3 \\ & s = t^d\ \text{mod}\ n_2 \\ & m = s^d\ \text{mod}\ n_1. \end{aligned}$$
At the very beginning, we are only given $c_0 := \mathcal{E}(m_0)$ where $m_0$ is the flag. We are then given three calls, in total, to the below oracles:
- [Encrypt] Given $m \geq 0$, return $\mathcal{E}(m)$, and
- [Decrypt] Given $c \geq 0$ and $c \neq c_0$, return $\mathcal{D}(c)$.
The objective is to recover $m_0$.
Solution⌗
📘 Notations. We will use $m_i$, $s_i$, $t_i$ and $c_i$ to denote the intermediate values in the $i$-th oracle call. That said, they satisfy
$$s_i = {m_i}^e\ \text{mod}\ n_1, \quad t_i = {s_i}^e\ \text{mod}\ n_2, \quad c_i = {t_i}^e\ \text{mod}\ n_3.$$
Recovering $n_1$⌗
Since $n_1$ is 2048 bits, it must satisfy $0 \leq n_1 < 2^{2048}$. We can recover $n_1$ with two two oracle calls:
- $c_1 := \mathcal{E}(2^{2048})$,
- $m_2 := \mathcal{D}(c_1)$.
With these oracle calls, we have $m_2 = 2^{2048} \ \text{mod} \ n_1$.
| $i$ | Direction | $m_i$ | $s_i$ | $t_i$ | $c_i$ |
|---|---|---|---|---|---|
| 1 | $m_1 \rightarrow c_1$ | $2^{2048}$ | - | - | $c_1$ |
| 2 | $m_2 \leftarrow c_2$ | $2^{2048}\ \text{mod}\ n_1$ | - | - | $c_1$ |
Recovering $p$ and $q$⌗
We can decrypt $c_3 = 2^{65537}$ remotely to recover $q$. From the decryption flow, we have
$$t_3 \equiv {c_3}^d \equiv 2^{ed} \equiv 2 \ (\text{mod}\ n_3),$$
thus $t_3 = 2$. Since $q$ is a common factor of $n_1$ and $n_2$, we also have $s_3 \equiv {m_3}^e \ (\text{mod}\ q)$ and $t_3 \equiv {s_3}^e \ (\text{mod}\ q)$. Essentially we have ${m_3}^{e^2} \equiv {s_3}^e \equiv t_3 \equiv 2 \ (\text{mod}\ q)$, implying ${m_3}^{e^2} - 2$ is a multiple of $q$. Thus $u := ({m_3}^{e^2} - 2)\ \text{mod}\ n_1$ is also a multiple of $q$. We then can recover $q$ by $q = \text{gcd}(u, n_1)$. Also, $p = n_1 / q$.
| $i$ | Direction | $m_i$ | $s_i$ | $t_i$ | $c_i$ |
|---|---|---|---|---|---|
| 1 | $m_1 \rightarrow c_1$ | $2^{2048}$ | - | - | $c_1$ |
| 2 | $m_2 \leftarrow c_2$ | $2^{2048}\ \text{mod}\ n_1$ | - | - | $c_1$ |
| 3 | $m_3 \leftarrow c_3$ | $m_3$ | - | $2$ | $2^e$ |
Recovering $r$⌗
How do we recover $r$ to fully recover the private key? To recover $r$, we will need two multiples of $r$ and perform GCD. Although we have no oracle calls left, we can reuse the previous oracle calls.
We can actually compute $s_i$ because $m_i$ and $n_1$ are known.
| $i$ | Direction | $m_i$ | $s_i$ | $t_i$ | $c_i$ |
|---|---|---|---|---|---|
| 1 | $m_1 \rightarrow c_1$ | $2^{2048}$ | $s_1$ | - | $c_1$ |
| 2 | $m_2 \leftarrow c_2$ | $2^{2048}\ \text{mod}\ n_1$ | $s_2$ | - | $c_1$ |
| 3 | $m_3 \leftarrow c_3$ | $m_3$ | $s_3$ | $2$ | $2^e$ |
Since ${s_3}^e \equiv 2\ (\text{mod}\ n_2)$, we know that ${s_3}^e - 2$ is a multiple of $r$.
On the other hand, since $r$ is a common factor of $n_2$ and $n_3$, we have
$${s_1}^e \equiv t_1 \ (\text{mod}\ r), \qquad {t_1}^e \equiv c_1\ (\text{mod}\ r).$$
Thus ${s_1}^{e^2} \equiv {t_1}^e \equiv c_1 \ (\text{mod}\ r)$, and therefore ${s_1}^{e^2} - c_1$ is also a multiple of $r$. We can do $\text{gcd}({s_1}^{e^2} - c_1, {s_3}^e - 2)$ to recover $r$, but ${s_1}^{e^2}$ is too large to compute. Luckily, ${s_3}^e$ is around $2^{27}$ bits so it is still computable. In this case, we can compute the required GCD by doing one step of Euclidean algorithm manually. Instead of sending ${s_1}^{e^2} - c_1$ as one of the parameters for GCD, we use $({s_1}^{e^2} - c_1) \ \text{mod}\ ({s_3}^e - 2)$.
Finally, we have $p$, $q$ and $r$ and therefore can decrypt the encrypted flag:
hkcert23{c4n_y0u_s01v3_th3_ch4l13n9e_wh3n_th3_encryp71on_0r4c13_1s_r3m0ved?}